Reincarnation

正因为梦易碎，才格外美好。

非递归式线段树（zkw线段树）

发表于 更新于 分类于 ，
本文字数： 6.9k 阅读时长 ≈ 6 分钟

人傻常数大，胸牌抱回家。

再谈线段树

我们所常知的线段树，是一种基于分治和递归的数据结构，通过合并子区间来得到答案，具有合并性，操作时间复杂度为 ，空间复杂度为 。

但由于众所周知的原因，递归的常数会比递推大很多，这也是线段树常数远远大于树状数组的原因（两者时间复杂度皆为 ）。

所以，或许我们可以深挖线段树的性质来优化下常数。

非递归式线段树

zkw线段树

由清华大学的张昆玮研究出的不基于递归与分治的线段树，常数极小，码量也较小。但扩展性（可做性）没有递归式线段树优秀。一般称为 线段树。

理论上来讲， 搭配标记永久化能够做所有普通线段树能做的事情，但有些会导致码量超标或者思路复杂。起到反效果。

运行形式

我们深究线段树的性质，发现一些比较巧妙的事，如当 时，线段树呈现下面的样子：

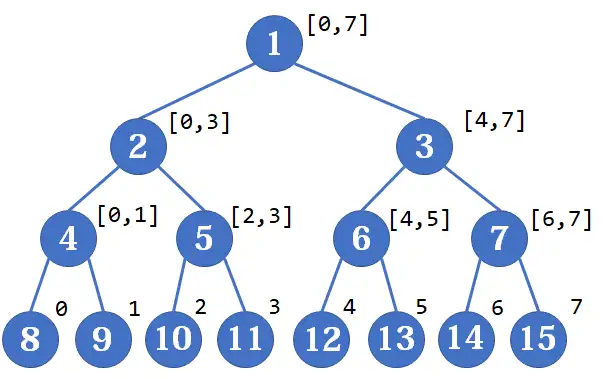
容易发现，每一个叶结点对应的线段树结点满足 的性质，而其余结点同样满足 倍关系。

但不仅仅与此，一棵满二叉树构造的线段树还有以下性质：

  • 整棵树有 个结点；
  • 一共有 层，第 层有 个结点，表示线段长度为 ，其中 。
  • 如果 为兄弟结点（位于同一层），则有 。
  • 左儿子结点编号为奇数，右儿子结点编号为偶数。

但很可惜的是，这些性质都局限于了 的情况。但我们也不可能不用啊，所以，我们将这些性质扩充到能够用的地方，所以考虑将 扩展为 。然后据此用非递归式建树。

操作实现

注意一点是， 支持的区间查询操作是开区间，意味着传入的 实际上返回的是 的区间权值，这意味着对于区间 的询问我们实际上要求 ，这要求我们要把 的结点建出，所以我们得到的 应当满足 。

建树

可以省去 struct 和原数组，直接对线段树数组进行赋值。

参考实现
 
1
2
3
4
5
6
inline void build()
{
	while(Len<=N+1) Len<<=1;
	for(int i=1;i<=N;++i) read(Tr[Len+i]);
	for(int i=Len-1;i>=1;--i) Tr[i]=Tr[i<<1]+Tr[i<<1|1];
}

单点修改

直接进行暴力 pushup ，可以在 时间内解决。

参考实现
 
1
2
inline void modifyX(int x,int v)
{ for(int i=Len+x;i;i>>=1) Tr[i]+=v; }

单点修改区间查询

这里以查询区间和为例，回收伏笔，我们要求将 内的所有值都被计算，也就是要求 的所有值都不被计算。

所以我们在线段树的叶结点上建立两个指针 ，让 向上传递。容易发现，如果 是其父结点的左子结点，则其右结点所表示的区间一定在 内， 同理。

但显然地，当 的时候，上述性质就出问题了，所以，我们向上传递的结束标记就是 。

参考实现
 
1
2
3
4
5
6
7
8
9
10
inline int querySum(int l,int r)
{
	int res=0;
	for(l+=Len-1,r+=Len+1;l^r^1;l>>=1,r>>=1)
	{
		if(~l&1) res+=Tr[l^1];
		if(r&1) res+=Tr[r^1];
	}
	return res;
}

区间修改

容易发现，逆向操作的 在 pushdown 的时候很难实现，毕竟是由下至上的传递。所以需要用到万恶的标记永久化，这个操作我们在分块的时候也提及到过。

对于每一个结点记录 add[] 表示当前结点曾经被修改过的和。但容易发现，按照上述区间修改的操作来讲，我们并不保证该区间是被完整访问的，这也是线段树需要拆分区间的原因，所以我们需要记录一个 来看对于当前这个结点实际上包含了多少个位置，当然，也可以开一个 std::pair 来保存该结点所表示的区间，但那样就体现不出 的优势了（虽然区间操作上 本身就没有什么优势）。

参考实现
 
1
2
3
4
5
6
7
8
9
10
11
inline void modifyAdd(int l,int r,ll v)
{
	ll ln=0,rn=0,num=1;
	for(l+=Len-1,r+=Len+1;l^r^1;l>>=1,r>>=1,num<<=1)
	{
		Tr[l]+=v*ln,Tr[r]+=v*rn;
		if(~l&1) Add[l^1]+=v,Tr[l^1]+=v*num,ln+=num;
		if(r&1) Add[r^1]+=v,Tr[r^1]+=v*num,rn+=num;
	}
	for(;l;l>>=1,r>>=1) Tr[l]+=v*ln,Tr[r]+=v*rn;
}

注意到，这一次的向上传递必须要到达根结点，因为区间修改下并不保证会在该子区间停止。

区间修改区间查询

同理区间修改，把 add[] 整上 ln,rn 后加入答案。

参考实现
 
1
2
3
4
5
6
7
8
9
10
11
12
13
inline ll querySum(int l,int r)
{
	ll ln=0,rn=0,num=1,res=0;
	for(l+=Len-1,r+=Len+1;l^r^1;l>>=1,r>>=1,num<<=1)
	{
		if(Add[l]) res+=Add[l]*ln;
		if(Add[r]) res+=Add[r]*rn;
		if(~l&1) res+=Tr[l^1],ln+=num;
		if(r&1) res+=Tr[r^1],rn+=num;
	}
	for(;l;l>>=1,r>>=1) res+=Add[l]*ln+Add[r]*rn;
	return res;
}

扩展

zkw 求最大子段和

题目简介

题目名称：小白逛公园
题目来源：

评测链接：https://www.luogu.com.cn/problem/P4513

形式化题意：给定一个长度为 的序列，维护 个操作：

  1. ，将
  2. ，求

数据范围：

这是一个极其经典的线段树的题，当然也可以用 来解决。

对于普通线段树而言，我们需要维护 ，表示当前区间的取了左端点的区间最大子段和，取了右端点的区间最大子段和，整个区间的区间最大子段和，区间和。

合并时，令 。

则有：

可以在 的时间内得到答案。

这一次让我们尝试用 来解决这个问题。单点修改加上区间询问，常规操作，但评测之后就会发现——挂得很惨？为什么呢？

容易发现，区间最大子段和的合并是有优先级的，这个优先级并没有体现在运算中，而是左和右的优先级上，我们需要的是左端点的 和右端点的 。如果我们将转移下标传反的话，就会造成答案上的错误。而递归式线段树恰恰保证了这一点，相同地， 并没有保证这一点。

所以我们需要运用一些手段使其满足这一点。常用的方法是，将所有需要计算的区间存储下来，然后从左往右（或者从右往左）依次进行合并。左端点用 std::queue，右端点用 std::stack，就可以保证这一点。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
// ----- Eternally question-----
// Problem: P4513 小白逛公园
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4513
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// Written by: Eternity
// Time: 2023-01-29 14:40:31
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ putchar(x?'1':'0'); }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=5e5+10;
const int INF=0x3f3f3f3f;
int N,Q,a[MAXN],Len;
struct St
{
	int lx,rx,val,sum;
	St(int lx=0,int rx=0,int val=0,int sum=0):
		lx(lx),rx(rx),val(val),sum(sum){}
}Tr[MAXN<<2];
std::queue<int>pre;
std::stack<int>suf;
inline St merge(St ls,St rs)
{
	St p;
	p.lx=std::max(ls.lx,ls.sum+rs.lx),p.rx=std::max(rs.rx,rs.sum+ls.rx);
	p.val=std::max(std::max(ls.val,rs.val),ls.rx+rs.lx),p.sum=ls.sum+rs.sum;
	return p;
}
inline void build(int n)
{
	Len=1;
	while(Len<=n+1) Len<<=1;
	for(int i=1;i<=n;++i) Tr[i+Len]=St(a[i],a[i],a[i],a[i]);
	for(int i=Len-1;i;--i) Tr[i]=merge(Tr[i<<1],Tr[i<<1|1]);
}
inline void modifyX(int x,int v)
{
	Tr[x+Len]=St(v,v,v,v);
	for(int i=(x+Len)>>1;i;i>>=1) Tr[i]=merge(Tr[i<<1],Tr[i<<1|1]);
}
inline int query(int l,int r)
{
	for(l+=Len-1,r+=Len+1;l^r^1;l>>=1,r>>=1)
	{
		if(~l&1) pre.push(l^1);
		if(r&1) suf.push(r^1);
	}
	St res=St(-INF,-INF,-INF,0);
	while(!pre.empty())
	{
		res=merge(res,Tr[pre.front()]);
		pre.pop();
	}
	while(!suf.empty())
	{
		res=merge(res,Tr[suf.top()]);
		suf.pop();
	}
	return res.val;
}
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(N,Q);
	for(int i=1;i<=N;++i) read(a[i]);
	build(N);
	for(int opt,ql,qr;Q--;)
	{
		read(opt,ql,qr);
		if(opt==1)
		{
			if(ql>qr) std::swap(ql,qr);
			write(query(ql,qr),'\n');
		} 
		else modifyX(ql,qr);
	}
	return 0;
}
/*

*/
相关文章