Reincarnation

正因为梦易碎，才格外美好。

多项式卷积与莫比乌斯 / 沃尔什变换

发表于 更新于 分类于 ，
本文字数： 9.2k 阅读时长 ≈ 8 分钟

“唯有一日的远观山峦，你可以赞叹其巍岩绝壁；而终会到来的绝日山巅，你将能领略世间万物。”

再论卷积

存在一个序列表示为 ，如果存在一个多项式，是该序列中的元素一一映射入该多项式的系数中，则该多项式称为该序列的生成函数。如上，则多项式 则为序列 的生成函数。

卷积即为生成函数的乘积在对应序列的变换上的的抽象。

对于序列 （多项式 ）其卷积序列（多项式）满足：

注意：序列与序列卷积得到的结果就是一个序列，多项式与多项式卷积得到的就是多项式。

我们已经学习了 等能够快速计算卷积的快速变换，而其中， 计算的是循环卷积，也就是形如：

的卷积，其中 为序列长度。

卷积的基本性质

本文仅对较为困难的性质进行证明，默认读者已经熟练掌握了至少初中数学的所有知识。

  • 卷积具有交换律，即 。
  • 卷积具有结合律，即
  • 卷积具有分配律，即

    证明：设 ，则有：

这些都是卷积的基本性质，很好证明，当然也很好理解，但这也同样不是我们今天研究的重点。

广义卷积

正如矩乘是 形式，而广义矩乘是 ，甚至其它各种变式，那对于卷积的 ，也存在一种变式呢。

答案是显然的，我们定义一种位运算卷积表示为 ，其中 ，表现为：，当然，我们也可以把 换成 之类的，也可以把 换成 等，组合方式很多，广义卷积的定义也就很多。

当然，大部分的这些广义卷积也满足交换律，结合律，分配律等基本性质。位运算卷积也在其中。

针对位运算卷积的快速变换

考虑以下这个问题：

题目简介

给定两个长度为 的序列 ，设序列 满足：

求当 时，序列 的值，对 取模。

数据范围：

这里需要求解的是广义卷积，用 是无法解决的。所以我们考虑用另外的方法来求解。

我们考虑在集合意义下作一个前缀和，类似于子集求和的 类，记录 ，也就是 在二进制集合下的所有子集。那我们考虑结合需要求的式子：

所以，我们可以在 的时间进行 的运算，这个思想就类似于多项式卷积中将系数表示法转换为点表示法进行运算。

快速沃尔什变换（FWT）

我们已经可以用线性时间得到 ，但对于每一个 ，我们却需要枚举子集来解决，这样的时间复杂度会巨量超标，所以，现在的问题在于如何快速求解 。

或卷积

考虑一种分治求解的思路，我们将这个函数表示为：

将 分为 前后两端，表示为 ，但事实上，对于 二进制位的最高位，，这是我们保证 被二分的前提，那这样的话 的子集就是其本身，但是上 应该当是包含了 部分，也就是 的部分，所以，真正的 应当表示为：

逆变换同理：

时间复杂度可以优化到 。

与卷积

同理于或卷积，我们同样利用分治来解决，得到的式子为：

异或卷积

这是最常用的 变换形式，但是和 有所不同，我们引入以下一个引理：

设 表示 在二进制位下的奇偶性，我们可以得到以下性质：

简单来讲，就是一个变式的结合律。

因此有

此时依然满足 。

得到结论为：

然后我们就用 解决了这个问题了。

完整实现

参考写法
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void Or(int a[],int inv)
{
	for(int mid=1;mid<Tot;mid<<=1)
		for(int i=0;i<Tot;i+=mid*2)
			for(int j=0;j<mid;++j)
				a[i+j+mid]=((a[i+j+mid]+inv*a[i+j])%P+P)%P;
}
void And(int a[],int inv)
{
	for(int mid=1;mid<Tot;mid<<=1)
		for(int i=0;i<Tot;i+=mid*2)
			for(int j=0;j<mid;++j)
				a[i+j]=((a[i+j]+inv*a[i+j+mid])%P+P)%P;
}
void Xor(int a[],int inv)
{
	for(int mid=1;mid<Tot;mid<<=1)
		for(int i=0;i<Tot;i+=mid*2)
			for(int j=0;j<mid;++j)
			{
				int x=a[i+j],y=a[i+j+mid];
				a[i+j]=(x+y)%P,a[i+j+mid]=((x-y)%P+P)%P;
				if(inv==-1)
				{
					a[i+j]=1ll*a[i+j]*Inv%P;
					a[i+j+mid]=1ll*a[i+j+mid]*Inv%P;
				}
			}
}

快速莫比乌斯变换（FMT）

仅能解决与卷积和或卷积，常数较高，但实现相比 更为简洁。

在 的求解中，我们曾经考虑过一个子集求和的问题，这与我们今天要探究的序列卷积有些许类似，也许可以从这方面入手。

下图表示了的是每一个 所对应的 和：

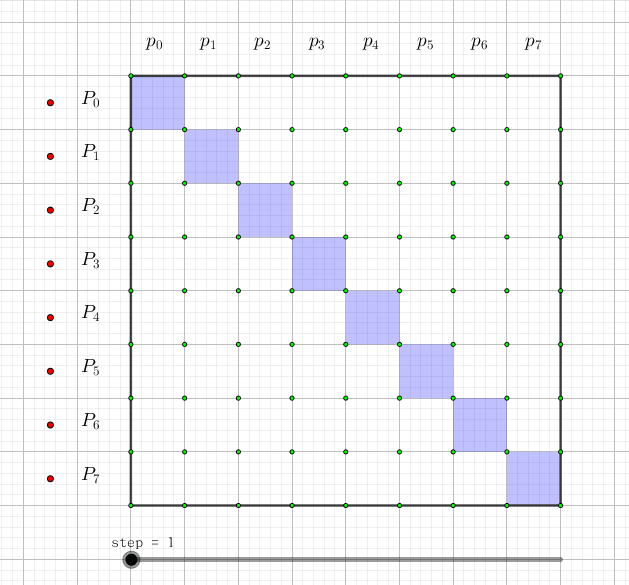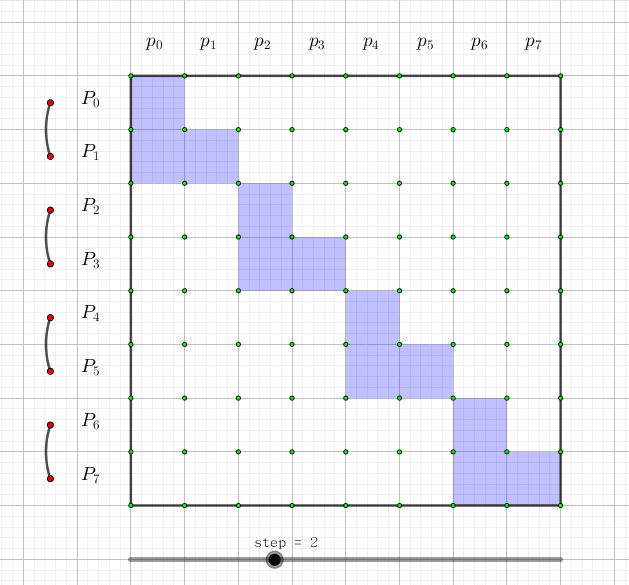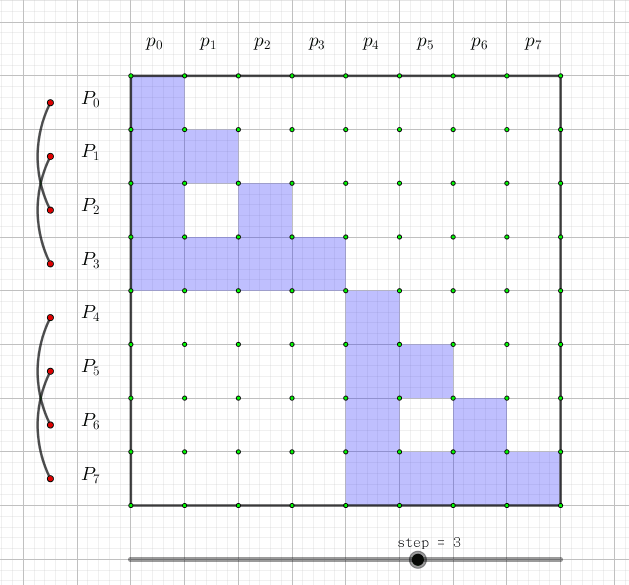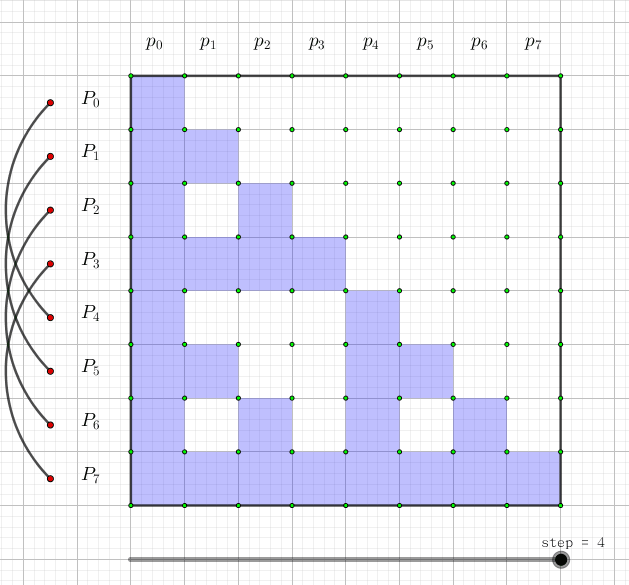
图片来自：https://yhx-12243.github.io/OI-transit/records/vijos%20%234.html

我们按照 的思想，设立：

可以发现，与或的区别也就是子集与逆子集的区别。

而对于其逆变换，也称为快速莫比乌斯反演（），似乎与莫比乌斯反演没有什么太大的关系。

考虑 的式子：

如果对其进行逆变换的话，涉及到一个容斥，即枚举子集的反集，会涉及到的问题，得到：

但代码实现比较简单，下面是 和 的整合版本。

参考代码
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
namespace Mobius_Transform
{
	void Or(int a[],int inv)
	{
		for(int i=0;i<N;++i)	
			for(int s=0;s<Tot;++s)
				if(s>>i&1) a[s]=((a[s]+1ll*inv*a[s^(1<<i)])%P+P)%P;
	}
	void And(int a[],int inv)
	{
		for(int i=0;i<N;++i)
			for(int s=Tot-1;~s;--s)
				if((~s)>>i&1) a[s]=((a[s]+1ll*inv*a[s^(1<<i)])%P+P)%P;
	}
};

容易发现，其本质就是高维前缀和。

二者比较

根据主定理分析， 的时间复杂度都是 ，但二者的真正实现存在差异，以洛谷模板题为例（异或都用的是 实现）：

时空比较 快速沃尔什变换（） 快速莫比乌斯变换（）
时间
空间
优化下

可见，各有各优，各有各劣。

快速子集变换（FST）

快速子集变换（）是 的一个变种，用于求解状态不重复子集交卷积问题。可以用 实现。

题目简介

题目名称：子集卷积
题目来源：

评测链接：https://www.luogu.com.cn/problem/P6097

有 个长度为 的序列 ，求出一个序列 满足：

对 取模。

数据范围：

实现

我们化简式子，用子集形式写成：

这是一个变式的位运算卷积，所以我们还是可以用高维前缀和（）的思路来想，对于原来的 ，我们用 来代替原来的 ，记录为集合 中有 个元素的情况，那显然， 是一一对应了的。

令 表示二进制下的 有多少个 ，可以知道 。所以我们对所有的 都做一次 。

所以我们将其化简得到：

那对于我们需要求的序列，答案就是 。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
// ----- Eternally question-----
// Problem: P6097 【模板】子集卷积
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P6097
// Memory Limit: 512 MB
// Time Limit: 3000 ms
// Written by: Eternity
// Time: 2023-01-14 16:06:56
// ----- Endless solution-------

//该代码对FWT和FMT都进行了实现。

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ putchar(x?'1':'0'); }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=4e6+10,MAXS=21;
const int P=1e9+9;
int N,Tot;
int a[MAXS][MAXN],b[MAXS][MAXN];
int Bit[MAXN];
int ans[MAXS][MAXN];
inline void FWT(int a[],int inv)
{
	for(int mid=1;mid<Tot;mid<<=1)
		for(int i=0;i<Tot;i+=mid*2)
			for(int j=0;j<mid;++j)
				a[i+j+mid]=((a[i+j+mid]+1ll*inv*a[i+j]%P)%P+P)%P;
}
inline void FMT(int a[],int inv)
{
	for(int i=0;i<N;++i)
		for(int s=0;s<Tot;++s)
			if(s>>i&1) a[s]=((a[s]+1ll*inv*a[s^(1<<i)])%P+P)%P;
}
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(N);Tot=1<<N;
	for(int i=0;i<Tot;++i) Bit[i]=Bit[i>>1]+(i&1);
	for(int i=0;i<Tot;++i) read(a[Bit[i]][i]);
	for(int i=0;i<Tot;++i) read(b[Bit[i]][i]);
	// for(int i=0;i<=N;++i) FWT(a[i],1),FWT(b[i],1);
	// for(int i=0;i<=N;++i) FMT(a[i],1),FMT(b[i],1);
	for(int i=0;i<=N;++i)
	{
		for(int j=0;j<=i;++j)
			for(int k=0;k<Tot;++k)
				ans[i][k]=(ans[i][k]+1ll*a[j][k]*b[i-j][k]%P)%P;
		// FWT(ans[i],-1);
		// FMT(ans[i],-1);
	}
	for(int i=0;i<Tot;++i) write(ans[Bit[i]][i],' ');
	return 0;
}
/*

*/

FMT 和 FWT 的实现比较

时空比较 快速沃尔什变换（） 快速莫比乌斯变换（）
时间
空间
代码长度

可见，FWT有绝对优势。

相关文章