Reincarnation

正因为梦易碎，才格外美好。

极角排序 & 动态凸包

发表于 更新于 分类于 ，
本文字数： 975 阅读时长 ≈ 1 分钟

命运的种子深埋于凝固的土地，万事古已有之，而现在人类得以看清它们。

极角排序

在二维平面上，一般用 来表示一个坐标，即其横坐标和纵坐标，但我们也从角度的方面思考，得到了二维点的极坐标表示 ，其中的变化式为：

很明显，极坐标的组成就是向量 与 轴的夹角和其长度。在代码实现中 <cmath> 库具备了 std::arctan 函数，但这个函数的值域是 ，所以我们使用 <cmath> 库里的另外一个函数 std::atan2，其值域为 ，也就是 的准确值。

然后使用 std::sort 就可以直接进行排序得到结果，时间复杂度 。

还有一种方法是通过向量叉乘与象限判断来排序，但这个方法个人觉得有点复杂化了，需要进行二维偏序计算，所以不建议使用。

需要注意的是，作极角排序之前需要确定极点，也就是参照点，一般都设为原点 。

参考实现
 
1
2
3
4
5
6
7
8
int cx=0,cy=0;
struct Point
{
    int x,y;
    double ang;
    inline void insert(int x,int y){ x=x,y=y,ang=std::atan2(y-cy,x-cx); }
    bool operator<(const Point &a) const { return ang==a.ang?x<a.x:ang<a.ang; }
};

两个方法的比较就是 std::atan2 会有精度缺失，而极角排序的常数极大。

例题

题目简介

题目名称：

题目来源：

评测链接：https://codeforces.com/contest/598/problem/C

形式化题意：给定 个向量 ，记两个向量组成的夹角为 ，求：

的 $i,j$，此处 $\alpha_{i,j}\in[0,\pi)$。

数据范围：$2\leq n\leq 10^5,|x_i|,|y_i|\leq 10^4,x^2_i+y^2_i>0$

考虑贪心，答案一定是两个相邻的向量，而相邻的向量，极角要么也相邻，要么就差值最大（即越过了 $x$ 轴的两条）。所以考虑首先实现极角排序，然后如何比较向量夹角。

我们知道：

而在 区间里， 单调递减，所以可以直接比较 。

至于 的计算里有乘法，所以我们变换式子删去乘法，又因为 的计算带根号，所以我们进行平方处理，平方处理记住要不等式换边，以及还有将负号提取出来。

最后的计算是 级别的，所以用 __int128_t。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
// ----- Eternally question-----
// Problem: C. Nearest vectors
// Contest: Codeforces - Educational Codeforces Round 1
// URL: https://codeforces.com/contest/598/problem/C
// Memory Limit:  256 MB
// Time Limit: 2000 ms
// Written by: Eternity
// Time: 2023-07-14 20:03:48
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
typedef long double ld;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ std::cout<<x; }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
using int128=__int128_t;
const int MAXN=1e5+10;
const long double pi=std::acos(-1);
int N;
struct Point
{
	int x,y,id;
	long double ang;
	bool operator<(const Point &_) const { return ang==_.ang?x<_.x:ang<_.ang; }
	inline long double len(){ return std::sqrt(x*x+y*y); }
}Pt[MAXN];
struct Angle
{
	Point a,b;
	int ida,idb;
	bool operator<(const Angle &arc) const
	{
		bool ok=0;
		ll pre=(ll)a.x*b.x+a.y*b.y,prec=(ll)(a.x*a.x+a.y*a.y)*(b.x*b.x+b.y*b.y);
		ll suc=(ll)arc.a.x*arc.b.x+arc.a.y*arc.b.y,sucf=(ll)(arc.a.x*arc.a.x+arc.a.y*arc.a.y)*(arc.b.x*arc.b.x+arc.b.y*arc.b.y);
		if(pre<0) prec*=-1,ok^=1;
		if(suc<0) sucf*=-1,ok^=1;
		return ok?((int128)pre*pre*sucf<(int128)suc*suc*prec):((int128)pre*pre*sucf>(int128)suc*suc*prec);
	}
}A[MAXN];
inline ll cross(Point a,Point b){ return (ll)a.x*b.x+a.y*b.y; }
inline long double angle(Point a,Point b)
{
	long double res=std::abs(b.ang-a.ang);
	if(res<-pi) res+=pi*2;
	return std::abs(res);
}
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(N);
	for(int i=1;i<=N;++i) read(Pt[i].x,Pt[i].y),Pt[i].ang=std::atan2(Pt[i].y,Pt[i].x),Pt[i].id=i;
	std::sort(Pt+1,Pt+N+1);
	for(int i=1;i<N;++i) A[i]=(Angle){Pt[i],Pt[i+1],Pt[i].id,Pt[i+1].id};
	A[N]=(Angle){Pt[N],Pt[1],Pt[N].id,Pt[1].id};
	std::sort(A+1,A+N+1);
	write(A[1].ida,' ',A[1].idb);
	return 0;
}

练习

极角排序与几何覆盖

题目简介

题目名称：

题目来源：

评测链接：https://www.spoj.com/problems/TRANSMIT/

形式化题意：给定一个圆点在 半径为 的半圆，你可以随意转动这个半圆。平面上存在 个点 ，求这个半圆最多能覆盖多少个点。多测。

数据范围：

考虑极角排序后用双指针扫描，注意把每个点的极角 复制一份加入到点集中，避免出现环上未统计。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
// ----- Eternally question-----
// Problem: TRANSMIT - Transmitters
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/SP898
// Memory Limit:  1 MB
// Time Limit: 127000 ms
// Written by: Eternity
// Time: 2023-07-15 08:24:23
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ std::cout<<x; }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=2e3+10;
const double pi=std::acos(-1);
int Cx,Cy,N;
double R;
struct Point
{
	int x,y,len2;
	double ang;
	bool operator<(const Point &_) const { return ang==_.ang?x<_.x:ang<_.ang; }
}Pt[MAXN];
inline int getDist(Point a,Point b){ return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y); }
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	while(true)
	{
		read(Cx,Cy),scanf("%lf",&R);
		if(R<0) break;
		read(N);
		for(int i=1;i<=N;++i)
		{
			read(Pt[i].x,Pt[i].y),Pt[i].ang=std::atan2(Pt[i].y-Cy,Pt[i].x-Cx);
			Pt[i+N].ang=Pt[i].ang+2*pi,Pt[i+N].x=Pt[i].x,Pt[i+N].y=Pt[i].y;
		}
		std::sort(Pt+1,Pt+N+N+1);N<<=1;
		for(int i=1;i<=N;++i) Pt[i].len2=getDist(Pt[i],{Cx,Cy});
		// for(int i=1;i<=N;++i,puts("")) write(Pt[i].x,' ',Pt[i].y),printf(" %.2lf %d",Pt[i].ang,Pt[i].len2);
		int l=1,r=1,cnt=(Pt[1].len2<=R*R),ans=0;
		for(;r<=N;++l)
		{
			if(r==N) break;
			while(r+1<=N&&Pt[r+1].ang-Pt[l].ang<=pi)
			{
				++r;
				if(Pt[r].len2<=R*R) ++cnt;
			}
			checkMax(ans,cnt);
			if(Pt[l].len2<=R*R) --cnt;
		}
		write(ans,'\n');
	}
	return 0;
}

极角排序与计算几何

题目简介

题目名称：

题目来源：

评测链接：https://www.luogu.com.cn/problem/P2992

形式化题意：在二维平面上有 个点 ，求三元组 使原点 在 组成的三角形内部的个数。保证没有任何一条由两个点组成的直线经过原点。

数据范围：

考虑求反集，否则得容斥。

三个点构成的三角形不包含原点的条件是其中两个点都在第三个点与原点的连线一侧，当然，也可能存在异侧但是不包含的情况，所以这是一个必要条件，而异侧的相对性也可以转换为同侧，这就是保证不重不漏而只计算一侧的方法。

考虑极角排序后维护双指针算区间即可，记得开 long long。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
// ----- Eternally question-----
// Problem: P2992 [USACO10OPEN] Triangle Counting G
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2992
// Memory Limit:  125 MB
// Time Limit: 1000 ms
// Written by: Eternity
// Time: 2023-07-15 15:22:43
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ std::cout<<x; }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=1e5+10;
int N;
struct Point
{
	int x,y;
	double ang;
	bool operator<(const Point &_) const { return ang==_.ang?x<_.x:ang<_.ang; }
}Pt[MAXN];
inline ll cross(Point a,Point b){ return (ll)a.x*b.y-(ll)a.y*b.x; }
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(N);
	for(int i=1;i<=N;++i) read(Pt[i].x,Pt[i].y),Pt[i].ang=std::atan2(Pt[i].y,Pt[i].x);
	std::sort(Pt+1,Pt+N+1);Pt[N+1]=Pt[1];
	ll ans=1ll*N*(N-1)*(N-2)/6,cnt=0;
	for(int i=1,suc=1;i<=N;++i)
	{
		while(cross(Pt[i],Pt[suc+1])>0) suc=(suc==N?1:suc+1),++cnt;
		ans-=(cnt-1)*cnt/2;--cnt;
	}
	write(ans);
	return 0;
}

动态凸包

考虑静态凸包的求法，有一个 扫描法和 算法，其中一个按照某一维排序，另外一个就是通过极角排序得到解，这两种方法都是可以扩展至动态加点维护凸包的。

Graham扫描法

我们以左下角的点作为极点（以 为第一关键字， 为第二关键字，这个点一定在凸包内），然后进行极角排序，然后将排序之后的点依次连接，会组成一个凹凸不定的多边形，此时我们进行调整，维护一个栈表示当前凸包上的点，在 时直接加入，否则我们将该点加入栈，然后比较栈顶的三个元素的旋转方向是否一致，是否符合三角形不等式，否则弹栈直到凸包合法。

Andrew算法

直接以 为第一关键字排序，后将排序结果依次相连，同样通过调整凹凸性可以存储凸包。

动态加点

我们这里假设已经有一个成型的凸包了，且忽视不必要且繁琐的边界，直接考虑算法本身（简称口胡），一种是基于点的分治，一种是基于边的分治。

对于点的分治，我们设当前需要加入的点为 ，我们找到最大的 使 ，并找到最小的 使 ，显然地，如果存在 的话，直接比较其纵坐标就可以了。

容易发现 就是 的前驱后继，此时我们将其连接，就可以形成新的凸包，但事实上，可能存在折线 不合法，所以我们从 向前删除所有不合法的点即可， 同理。

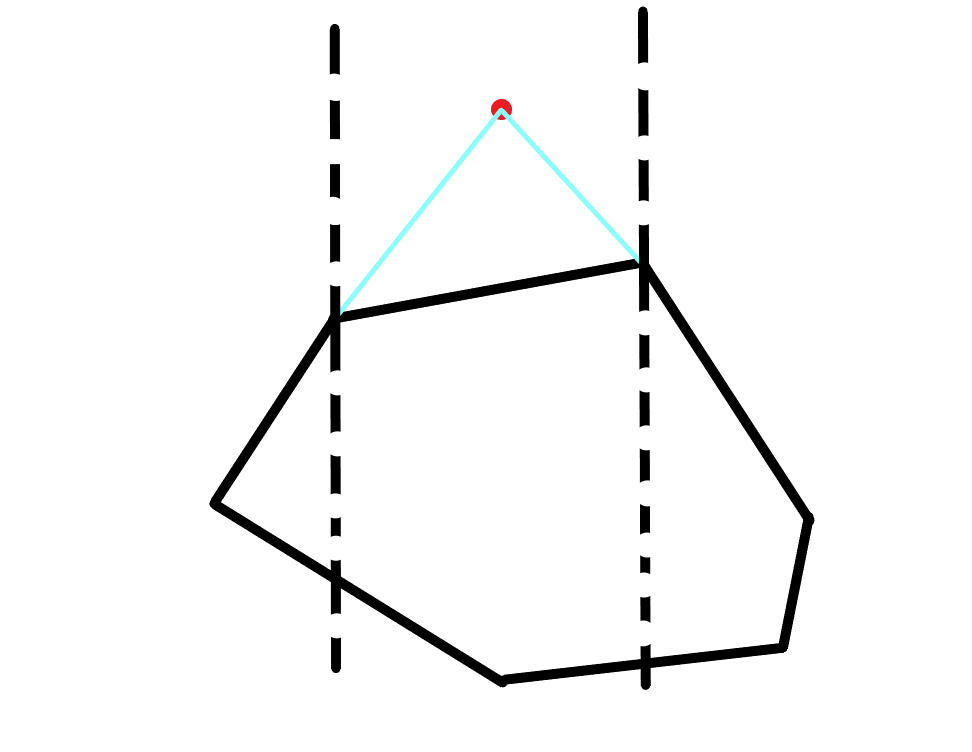
Point

这种方法可以使用平衡树维护，一般用 std::set。

基于边的分治是我口胡的，不保证正确性， 爷没举出反例，也没证，我写代码的时候发现边界太多索性放弃鸽了。

Edge

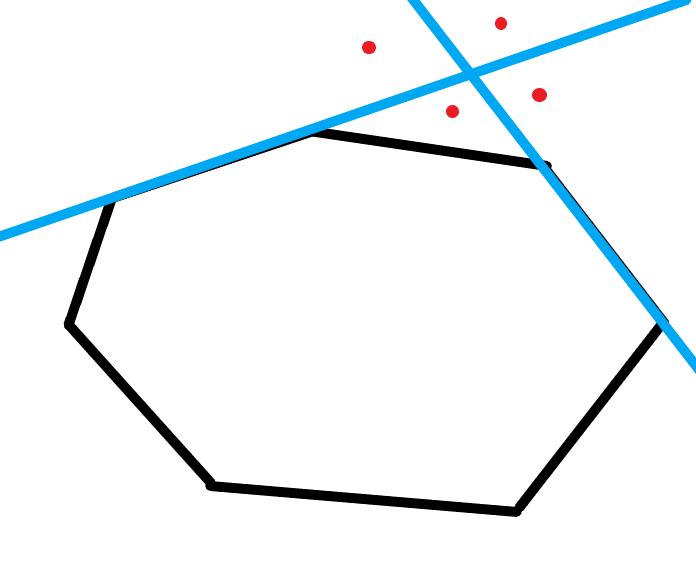
考虑图中的形式，以维护上凸包为例，我们分别找到该点左右的一条直线（由凸包线段扩展出的）满足这两条线段都在点的上方（用一般直线式即可判断），如果不存在则该点一定与左右边界点直接相连，然后舍弃这两条线段之间的所有点，并让两条线段直接与新点连接。下凸包同理。

感觉是一个很美丽的结论，但事实上写起代码来需要描述的边界很多，反正我是写不来（懒），读者大可一试。笔者在网上似乎没有找到相似的做法，读者找到的话也可以推荐给笔者。

例题

题目简介

题目名称：

题目来源：

评测链接：https://codeforces.com/problemset/problem/70/D

形式化题意：首先给出 个点，然后维护 个操作：

  1. 将 加入凸包。
  2. 询问 是否在凸包内。

数据范围：

考虑直接维护即可。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
// ----- Eternally question-----
// Problem: D. Professor's task
// Contest: Codeforces - Codeforces Beta Round 64
// URL: https://codeforces.com/problemset/problem/70/D
// Memory Limit:  256 MB
// Time Limit: 1000 ms
// Written by: Eternity
// Time: 2023-07-14 19:14:34
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ std::cout<<x; }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=1e5+10;
int Q;
struct Point
{
	int x,y;
	double ang;
	bool operator<(const Point &_) const { return ang==_.ang?x<_.x:ang<_.ang; }
	friend Point operator-(Point a,Point b){ return {a.x-b.x,a.y-b.y}; }
}Tri[4],Sum;
using stit=std::set<Point>::iterator;
std::set<Point>St;
std::set<Point>::iterator pre,suf;
inline ll cross(Point a,Point b){ return (ll)a.x*b.y-(ll)a.y*b.x; }
inline auto Pre(stit x){ return x==St.begin()?--St.end():--x; }
inline auto Suf(stit x){ return (++x)==St.end()?St.begin():x; }
inline void insert(Point p)
{
	if(cross(p-*pre,*suf-p)<=0) return ;
	St.insert(p);
	stit cur=St.find(p),pr=Pre(cur),ppr=Pre(pr);
	while(cross(*cur-*pr,*pr-*ppr)>=0) St.erase(pr),pr=ppr,ppr=Pre(ppr);
	stit sc=Suf(cur),ssc=Suf(sc);
	while(cross(*ssc-*sc,*sc-*cur)>=0) St.erase(sc),sc=ssc,ssc=Suf(ssc);
}
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(Q);Q-=3;
	for(int i=1,tmp;i<=3;++i)
	{
		read(tmp,Tri[i].x,Tri[i].y);
		Sum.x+=Tri[i].x,Sum.y+=Tri[i].y;
		Tri[i].x*=3,Tri[i].y*=3;
	}
	for(int i=1;i<=3;++i) Tri[i].ang=std::atan2(Tri[i].y-Sum.y,Tri[i].x-Sum.x),St.insert(Tri[i]);
	for(int opt,x,y;Q--;)
	{
		read(opt,x,y);x*=3,y*=3;
		Point p={x,y,std::atan2(y-Sum.y,x-Sum.x)};
		if((suf=St.lower_bound(p))==St.end()) suf=St.begin();
		pre=Pre(suf);
		if(opt==1) insert(p);
		else
		{
			if(cross(p-*pre,*suf-p)<=0) puts("YES");
			else puts("NO");
		}
	}
	return 0;
}
相关文章