下一刻,宇宙向我奔来。
闵可夫斯基和
有一说一,本来不是很想碰计算几何这一部分的,高中数学向量部分也学得烂,结果「第六分块」摆在面前告诉我需要《基础的计算几何意识》,而 也考了,所以就跑过来简单学学。
在二维平面中存在两个点集 ,那么这两个点集一定会分别形成一个凸包。现在我们需要求解 ,称之为点集的闵可夫斯基和,定义点集 ,那么 集合的组成为:
没错,虽然称之为闵可夫斯基和,但你发现 集合大小是 级别的,那是否存在方法使得 与 同级,这是显然的。
我们首先求出 的凸包,将凸包边记作 ,那么, 的凸包是将 归并后按照极角排序得到的封闭图形。这样的话, 的凸包是 级,也就是与 同级。
甚至用一种更加形象的解释,那就是将 中所有的点全部替换称由 点集组成的图形,然后对这个有 个点的抽象图形求凸包,就可以得到 的凸包。
闵可夫斯基和是针对点集的定义,但其运用可推广至流形的连续集,然后得到广域定义
:
将 集合沿着 的边际连续运动一周后扫过的区域与 集合本身的并集,
称之为 ,即 与 的闵可夫斯基和。
你发现就是上面的形象解释的数学语言,注意闵可夫斯基和满足交换律。
下面有一个例子:
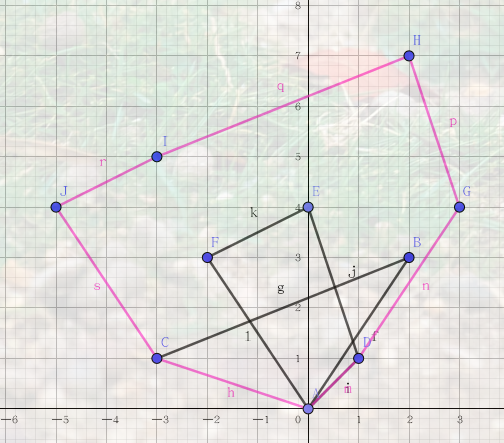
如果图片挂了可以去洛谷题解上找找。
求解
我们用向量 来表示凸包中的边,这有助于之后我们进行极角排序。
然后我们首先对 与 分别求取凸包,因为此时凸包向量已经按照极角排序结束,所以我们可以直接归并,注意归并后可能存在共线,所以需要再次求解凸包。所以事实上闵可夫斯基和的瓶颈在于求解凸包,时间复杂度 。
参考实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| inline int Convex(Point *a,int n)
{
for(int i=1;i<=n;++i) Stk[i]=a[i];
for(int i=2;i<=n;++i)
if(Stk[i].x<Stk[1].x||(Stk[i].x==Stk[1].x&&Stk[i].y<Stk[1].y)) std::swap(Stk[1],Stk[i]);
Ori=Stk[1];
std::sort(Stk+2,Stk+n+1,cmp);
int Top=1;
for(int i=2;i<=n;++i)
{
while(Top>=2&&(Stk[Top]-Stk[Top-1])*(Stk[i]-Stk[Top-1])<=0) --Top;
Stk[++Top]=Stk[i];
}
for(int i=1;i<=Top;++i) a[i]=Stk[i];
return Top;
}
inline int Mincowsky(Vector *a,Vector *b,int n,int m,Vector *c)
{
c[1]=Pt1[1]+Pt2[1];
int cur1=1,cur2=1,tot=1;
while(cur1<=n&&cur2<=m)
{
++tot;
if(a[cur1]*b[cur2]>=0) c[tot]=c[tot-1]+a[cur1++];
else c[tot]=c[tot-1]+b[cur2++];
}
while(cur1<=n) ++tot,c[tot]=c[tot-1]+a[cur1++];
while(cur2<=m) ++tot,c[tot]=c[tot-1]+b[cur2++];
while(tot>=2&&(c[tot]-c[tot-1])*(c[1]-c[tot-1])<=0) --tot;
return tot;
}
signed main()
{
N=Convex(Pt1,N),M=Convex(Pt2,M);
for(int i=1;i<=N-1;++i) Vec1[i]=Pt1[i+1]-Pt1[i];
for(int i=1;i<=M-1;++i) Vec2[i]=Pt2[i+1]-Pt2[i];
Vec1[N]=Pt1[1]-Pt1[N],Vec2[M]=Pt2[1]-Pt2[M];
Tot=Mincowsky(Vec1,Vec2,N,M,S);
}
|
例题
