Reincarnation

正因为梦易碎，才格外美好。

插入型dp

发表于 更新于 分类于 ，
本文字数： 15k 阅读时长 ≈ 13 分钟

生活会击穿流水的躯体，但他们的影子始终如一。

插入型dp

实际上经典分类中并不存在插入型 这一说，只是后来人们认为这一部分题目具有统一性而得到的名字。区别于区间 与线性 ，其状态设计确实不太寻常。

例题

题目简介

题目名称：

题目来源：

评测链接：https://www.luogu.com.cn/problem/P5999

形式化题意：给定 ，求出所有 的排列 满足：

  • ；
  • ；
  • 或 。

对 取模。

数据范围：

考虑到这是一个排列的话，如果我们记录 表示当前为第 个数，上一个数为 ，你并不知道前面已经填过的数的状态，所以并没有办法转移。

所以我们考虑不需要状压而需要将已经填过的数记录，那很显然有一种方法，我们将所有数以一种规定的顺序插入到整个排列中。具体来讲，我们现在有一个初始为空的 ，然后我们按照一定的顺序将 插入到 中并计算贡献。

所以我们这里考虑从小到大插入。

那么考虑插入途中，如果我们用 表示插入了数的位置，那么显然一个序列就会形成： 等等的形式，更简单来说，就是被填入的连续段。

所以我们考虑现在插入 可能会对序列形式产生的影响，设 插入到位置 ：

  • 如果 均未插入数，那么显然 会独自形成一个连续段，长度为 ；
  • 如果 存在数，而 没有（反转类似），那么 就会作为这个连续段的新的左右端点。
  • 如果 均插入了数，那么 的插入会合并这两个连续段，形成一个更长的连续段。

而最终状态，也就是所有数都已经被填入，那么就会形成一个长度为 的连续段。

所以我们从连续段来考虑设计状态，有 表示现在已经填入了 ，形成了 个连续段。

然后我们依然考虑上面的三种情况：

  • 新增连续段，那么这个新增的连续段对于原来的 个连续段有 个空位，也就是 。
  • 仅合并一端，那么对于左右端点，只能合并一边，而中间可以合并两边。但事实上，如果我们把 填入到连续段的端点上，其中一边一定是 的已经填入的 ，而另一端之后填入的无论是多少，一定大于 ，所以实际上这种情况不存在，或者不合法。
  • 然后就是合并两端的情况，一共有 个空位，所以 。

但我们有一种特殊情况并没有考虑进去，那就是 ，他们处于整个序列的端点， 都是空，所以此时，对于仅合并一端的情况下是合法的，所以我们需要对 进行特殊处理，也就是当 或 时，其转移方程应有所不同，具体如下：

因为此时 或 可能并没有被填入，所以可能新增一个连续段，也可能不会。

时间复杂度 。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
// ----- Eternally question-----
// Problem: P5999 [CEOI2016] kangaroo
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5999
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Written by: Eternity
// Time: 2023-10-05 15:41:21
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ putchar(x?'1':'0'); }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=2e3+10;
const int Mod=1e9+7;
template<class T1,class T2>
inline void add(T1 &x,T2 y){ x=x+y>=Mod?x+y-Mod:x+y; }
int N,S,T;
ll Dp[MAXN][MAXN];
signed main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(N,S,T);Dp[1][1]=1;
	for(int i=2;i<=N;++i)
	{
		if(i==S||i==T)
		{
			for(int j=1;j<=N;++j) add(Dp[i][j],(Dp[i-1][j-1]+Dp[i-1][j])%Mod);
		}
		else
		{
			for(int j=1;j<=N;++j)
			{
				add(Dp[i][j],Dp[i-1][j-1]*(j-(i>S)-(i>T))%Mod);
				add(Dp[i][j],Dp[i-1][j+1]*j%Mod);
			}
		}
	}
	write(Dp[N][1]);
	return 0;
}
/*

*/
AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
// ----- Eternally question-----
// Problem: P5999 [CEOI2016] kangaroo
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5999
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Written by: Eternity
// Time: 2023-10-07 15:43:04
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ putchar(x?'1':'0'); }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=2e3+10;
const int Mod=1e9+7;
template<class T1,class T2>
inline void add(T1 &x,T2 y){ x=x+y>=Mod?x+y-Mod:x+y; }
int N,S,T;
int Dp[MAXN][MAXN];
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(N,S,T);
	Dp[1][1]=1;
	for(int i=1;i<=N-1;++i)
	{
		if(i+1==S||i+1==T)
		{
			for(int j=1;j<=i;++j) add(Dp[i+1][j],Dp[i][j]),add(Dp[i+1][j+1],Dp[i][j]);
		}
		else
		{
			for(int j=1;j<=i;++j)
			{
				add(Dp[i+1][j+1],(ll)Dp[i][j]*(j+1-(i>=S)-(i>=T))%Mod);
				add(Dp[i+1][j-1],(ll)Dp[i][j]*(j-1)%Mod);
			}
		}
	}
	write(Dp[N][1]);
	return 0;
}
/*

*/

例题

排列求和

题目简介

题目名称：摩天大楼
题目来源：

评测链接 ：https://loj.ac/p/2743
评测链接 ：https://www.luogu.com.cn/problem/P9197

形式化题意：给定一个序列 ，求出所有 的排列 使得：

对 取模。

数据范围：

我们考虑从小到大向序列中插入 。

但考虑到插入型 的状态并不好维护，因为题目贡献与排列左右的数值有关。

我们考虑一个连续段，一定是一个单谷的函数，设这个连续段中最小元素为 ，左端点为 ，右端点 。那么这个连续段对权值和的贡献为 。

然后考虑这些贡献并不好维护，但这些贡献是独立的，所以我们考虑将其拆开维护。我们设当前总和为 。

首先考虑边界问题，在合并两个连续段时，边界会被更新，具体来讲，，因为当前插入的 会作为左右连续段的右端点和左端点，所以会贡献 次。但显然，如果当前插入的 属于 或者 ，则只会贡献 次。

然后用相同的方式考虑谷值，一个谷值只会在新增连续段的时候被更新，也就是 ，而类似地，如果当前新增段是序列头或序列尾，也只会贡献 次。

所以我们设计状态 表示当前插入了 （排序后的），一共有 个连续段，当前权值和为 ，对于左右端点，已经被插入的个数为 ，然后考虑转移：

  • 插入非边界连续段，。
  • 合并连续段，，该情况仅在 时转移。
  • 插入到非边界连续段端点处，，该情况仅当 时转移；
  • 作为一个新的边界连续段插入，，该情况仅当 时转移；
  • 作为边界连续段端点插入，，该情况仅当 时转移。

最终答案为 ，虽然第三维的答案贡献仅有 ，但是转移涉及到减法操作，所以必须转移 ，所以最后时间复杂度 。

我们观察其性质，拍到二维平面上。

img

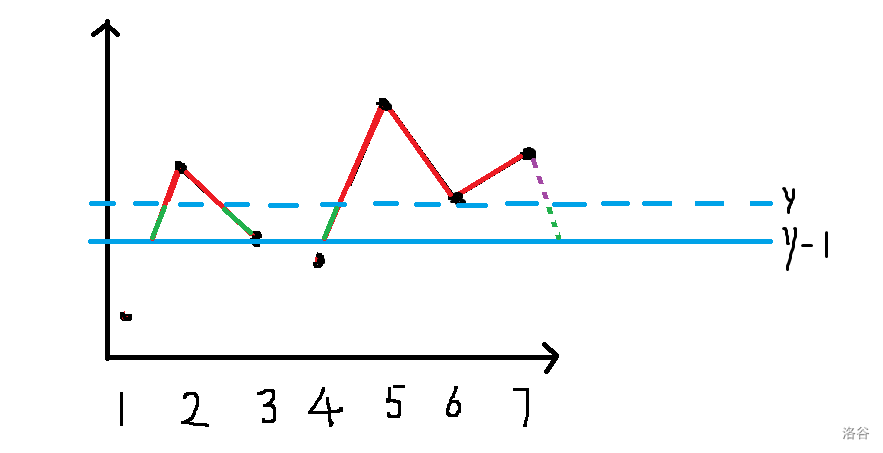
图片来自洛谷题解区

我们用微元贡献法，将每一个 差分成细微的数值变化，那么扫描线往上，每一段的贡献次数就是当前连续段的个数。

也就是对于 ，实际上拆分成 。

我们考虑建立权值哈希，设 为 进行重排列后的序列，并记 表示 在 序列中位置，也就是 ，那么上述贡献可以拆分成 。记 ，那么有

然后再乘上当前连续段的数量，即是贡献。

于是我们沿用上述状态，但是更换转移，记录 ：

  • 插入非边界连续段，；
  • 作为中间点合并连续段，，仅当 时转移。
  • 插入到非边界连续段端点处，，仅当 时转移。
  • 插入为边界连续段，，仅当 时转移；
  • 插入到边界连续段端点处，，仅当 时转移。

答案与上面一样。时间复杂度 。注意特判 。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
// ----- Eternally question-----
// Problem: P9197 [JOI Open 2016] 摩天大楼
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P9197
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// Written by: Eternity
// Time: 2023-10-07 11:32:06
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ putchar(x?'1':'0'); }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=1e2+10,MAXL=1e3+10,MAXS=1e5+10;
const int Mod=1e9+7;
template<class T1,class T2>
inline void add(T1 &x,T2 y){ x=x+y>=Mod?x+y-Mod:x+y; }
int N,L,val[MAXN];
int Dp[MAXN][MAXN][MAXL][3];
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(N,L);
	for(int i=1;i<=N;++i) read(val[i]);
	if(N==1) return puts("1"),0;
	std::sort(val+1,val+N+1);
	Dp[0][0][0][0]=1;
	for(int i=0;i<N;++i)
		for(int j=0;j<=i;++j)
			for(int k=0;k<=L;++k)
				for(int s=0;s<=2;++s)
				{
					int v=k+(val[i+1]-val[i])*(2*j-s);
					if(v>L) continue;
					add(Dp[i+1][j+1][v][s],(ll)Dp[i][j][k][s]*(j+1-s)%Mod);
					if(j>=2) add(Dp[i+1][j-1][v][s],(ll)Dp[i][j][k][s]*(j-1)%Mod);
					if(j>=1) add(Dp[i+1][j][v][s],(ll)Dp[i][j][k][s]*(2*j-s)%Mod);
					if(s<2) add(Dp[i+1][j+1][v][s+1],(ll)Dp[i][j][k][s]*(2-s)%Mod);
					if(s<2) add(Dp[i+1][j][v][s+1],(ll)Dp[i][j][k][s]*(2-s)%Mod);
				}
	int ans=0;
	for(int i=0;i<=L;++i) add(ans,Dp[N][1][i][2]);
	write(ans);
	return 0;
}
/*

*/

排列求和 II

题目简介

题目名称：波浪
题目来源：浙江省选

评测链接：https://www.luogu.com.cn/problem/P2612

形式化题意：给定 ，求出所有 的排列 满足：

求出随机一个排列满足上述条件的概率，保留小数点后 位。

数据范围：

乍一看和上面题差不多，仔细分析确实是这样。

考虑 太大，所以我们转为求出 的方案数，因为总和不超过 ，所以实际上复杂度不会超过 。

但是瓶颈在于 ，因为 long double 也只有 多位。但是我们有高贵的四精度。也就是 __float128，但是仅支持标准输入输出流，然后规定位数我们按照分数分治来求即可。也就是每次乘 再取个位。

注意直接计算可能会爆标，所以计算中途就除掉。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
// ----- Eternally question-----
// Problem: P2612 [ZJOI2012] 波浪
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2612
// Memory Limit: 125 MB
// Time Limit: 6000 ms
// Written by: Eternity
// Time: 2023-10-07 11:48:59
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ putchar(x?'1':'0'); }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
using Double=__float128;
const int MAXN=1e2+10,MAXM=5.05e3+10;
int N,M,K;
Double Dp[2][MAXN][MAXM][3];
inline void print(Double ans)
{
	// if(ans+1e-14>=1) return std::cout<<"1."<<std::string(K,'0'),void();
	std::cout<<"0.";ans*=10;
	for(int i=1;i<=K;++i)
	{
		std::cout<<(int)(ans+(K==i)*0.5);
		ans=(ans-(int)ans)*10;
	}
	return ;
}
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(N,M,K);
	int L=std::min(N*(N+1)/2,M-1);
	Dp[0][0][0][0]=1;
	for(int i=0,op=1;i<N;++i,op^=1)
	{
		std::memset(Dp[op],0,sizeof(Dp[op]));
		for(int j=0;j<=i;++j)
			for(int k=0;k<=L;++k)
				for(int s=0;s<=2;++s)
				{
					int v=k+2*j-s;
					Double res=Dp[op^1][j][k][s]/(i+1);
					if(v>L) continue;
					Dp[op][j+1][v][s]+=res*(j+1-s);
					if(j>=2) Dp[op][j-1][v][s]+=res*(j-1);
					if(j>=1) Dp[op][j][v][s]+=res*(2*j-s);
					if(s<=1) Dp[op][j+1][v][s+1]+=res*(2-s);
					if(s<=1) Dp[op][j][v][s+1]+=res*(2-s);
				}
	}
	Double ans=0;
	for(int i=0;i<=L;++i) ans+=Dp[N&1][1][i][2];
	print(1-ans);
	return 0;
}
/*

*/
相关文章