图——连通性相关

“无法僭越的鸿沟终无法达到少年的彼岸，曾几何时的奔赴却依然无悔恋爱的谎言。”

图论基本概念

对于结点，边，度数以及无向图，有向图这些概念想必都会，可以参考 来学习，这里讲一些与连通性有关的基本知识。

连通

无向图

对于一个点对 ，说 连通当且仅当 和 之间能够通过一些边和结点（可以没有中转结点）到达。

根据上述定义，我们可以得出：任意结点与自身连通，每一条边的两个端点连通。

对于一个无向图 ，如果不存在一个点对 不连通，则称 为连通图（），并称 是具有连通性（）的。

有向图

在有向图中，无向图里的连通概念被称为可达，且不满足可逆性，即 可达不一定能推出 可达。

如果一张有向图 ，满足对于 可以两两互相可达，则 是强连通（），且 是强连通图（）；另外，如果将 中所有的有向边替换为无向边之后 变成了连通图，则称有向图 是弱连通（），且 是弱连通图（）。

连通分量

若 是 的一个连通子图，且不存在 满足 且 为连通图，则 是 的一个连通块 / 连通分量（）（极大连通子图）。

对于一张图 ，若有其子图 是连通的，且没有 且 是连通图，则称 是 的连通分量。

显而易见的，连通图的连通分量是本身。

然后对于连通性图的算法，包含有强连通分量（针对有向图）和双连通分量（针对无向图）两者，这些我们之后再谈。

---

割点 / 割边

运用范围

该概念仅针对无向图。

一个点被称为割点（又称割顶），当且仅当删除这个点即与之连接的所有边之后，整张图的连通分量增加。（形式化来讲，当该结点及其连边被删除后，存在两个点 本来连通现在不连通）

一条边被称为割边，当且仅当删除这条边之后，整张图的连通分量增加。（形式化来讲，当该边被删除后，存在两个点 本来连通现在不连通）

---

缩点

该算法适用于有向图。

其实现在于，能在 的时间内将所有的有向环压缩成一个点，并得到这张图的强连通分量个数即编号。

我们考虑一种名为 的算法（与求 的那个算法不同）。

关于 Tarjan

全名为 ，生于 年的美国加州波莫纳，计算机科学家。

在 界广为流传的名为 算法，有求树上最近公共祖先（），求强连通分量，求边（点）双连通分量。

不仅如此，我们使用的并查集（）、伸展平衡树（）、动态树 也是 发明的。

这个算法的能够带给我们的方式显然——通过缩点得到一个有向无环图，即 ，而显然的， 的性质会比普通图性质强许多（虽然还是有些难做）。

Tarjan 实现

我们考虑环对于其它类型的图有什么特殊的地方，如果我们对一条环进行 的话，我们会在一次搜索中到相同的结点很多次（这也是 判负环的方法），那我们考虑从这个地方入手。

记录两个东西：dfn[] 和 low[] 分别表示第 个结点是对于整个图而言第 dfn[x] 个搜到的，而 low[] 表示当我们第一次搜到 之后所有到达的结点中，找到的 dfn[] 值最小的。

这两个函数能够带给我们的东西也很明了了，我们如果用 dfs 来遍历整个图的话，对于一个环，除了我们第一次到达环的地方，其它结点必定满足 的性质，因为这个结点必定会达到环上已经经过了的结点，这是显然的。而对于环上初结点，也必然满足的是 的性质。

在对整个图进行 dfs 遍历的时候，我们维护一个栈 ，描述当前已经被遍历过且没有被划分在之前的强连通分量的结点，我们假设在走到当前环之前的所有结点都已经被划分正确，那么现在栈中所剩下的结点必然就会属于当前环，也就是当前的强连通分量，也就可以被缩成一个点。

我们可以这样写伪代码：

$$\begin{align} &function:Tarjan(x)\nonumber \\ &\quad init\rightarrow dfn,low=new\{cnt\},instack\leftarrow x \nonumber \\ &\quad for(v\leftarrow x)\ edge \nonumber \\ &\quad\quad if(v\ hasn's\ been\ visited) \nonumber \\ &\quad\quad\quad then\ Tarjan(v) \nonumber \\ &\quad\quad\quad checkmin\{ low[u],low[v] \} \nonumber \\ &\quad\quad else\ if(v\ is\ in\ the\ stack) \nonumber \\ &\quad\quad\quad then\ checkmin\{ low[u],dfn[v] \} \nonumber \\ &\quad endfor \nonumber \end{align}$$

伪代码不太清晰。

我们贴代码来详细说明：

参考代码

int Dfn[MAXN],Low[MAXN],Stk[MAXN],Cnt,Top;
bool Ins[MAXN];
int Sizc[MAXN],Scc[MAXN],Sc;
void Tarjan(int x)
{
    Dfn[x]=Low[x]=++Cnt,Stk[++Top]=x,Ins[x]=1;
    for(int e=Head[x],v;e;e=Edge[e].next)
    {
        if(!Dfn[v=Edge[e].to])
        {
            Tarjan(v);
            checkMin(Low[x],Low[v]);
		}
        else if(Ins[v]) checkMin(Low[x],Dfn[v]);
    }
    if(Dfn[x]==Low[x])
    {
        Scc[x]=++Sc;
        while(Stk[Top]!=x)
        {
            Scc[Stk[Top]]=Sc,++Sizc[Sc];
            Ins[Stk[Top]]=0,--Top;
        }
        Scc[x]=Sc,++Sizc[Sc],Ins[x]=0,--Top;
    }
}
// int main() for(int i=1;i<=N;++i) if(!Dfn[i]) Tarjan(i);

整个 dfs 遍历分为两个部分——一是遍历，二是划分，按照我们前文说的来做。

第一个部分在于处理 dfn[] 和 low[] ，而第二个部分就是通过处理的 dfn[],low[] 来得到每一个强连通分量的信息，申明定义：

• 表示原来编号为 的结点现在属于第 个强连通分量；
• 表示编号为 的强连通分量的结点个数；
• 表示缩点之后原来的有向图的强连通分量个数。
• 主函数那个主要是避免原图不是连通图。

保证按照上述方法建出的缩点新图为 。

---

其它方法

另有两种方法求出强连通分量—— 算法和 算法。

两者的实现相比起 都略有一些麻烦。（个人意见）且实现方法都有些类似，有需要的读者可以在 上得到相关资料，这里不多阐述。

---

例题

都比较板，大概就是缩点 一些 上 或者图论算法。

P2863 [USACO06JAN]The Cow Prom S

甚至翻译都给你提示了，这就是个板子，不贴代码了。

---

P2746 [USACO5.3]校园网Network of Schools

对于子任务 ，求的就是缩点之后入度为 的结点个数；对于子任务 ，求的是缩点之后 入度为 和出度为 的结点个数的 ，注意要特判整个图都是一个强连通分量的情况。

---

P2169 正则表达式

有题解 。

---

P2656 采蘑菇

对于每一条边，它有三种贡献：

• 不贡献，即最优解没有通过这条边；
• 贡献最大的一次，这条边只被走过一次；
• 贡献了很多次，这条边被走了很多次。

这是一个有向图，那么一条边被走很多次的充要条件是其在一个强连通分量里，那么这个强连通分量里的所有边都可以被“榨干”，那就考虑缩点，然后运用 跑最长路即可。

AC Code

// ----- Eternally question-----
// Problem: P2656 采蘑菇
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2656
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Written by: Eternity
// Time: 2022-11-06 15:24:15
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ std::cout<<x; }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=8e4+10,MAXM=2e5+10;
int N,M,St;
struct G
{
	int next,to,val;
}Edge[MAXM<<1];
int Head[MAXN],Total;
inline void addEdge(int u,int v,int w)
{
	Edge[++Total]=(G){Head[u],v,w};Head[u]=Total;
	// Edge[++Total]=(G){Head[v],u,w};Head[v]=Total;
}
int Dfn[MAXN],Low[MAXN],Stk[MAXN],Top;
bool Ins[MAXN];
int Scc[MAXN],Cnt,Sc,Sizc[MAXN];
void Tarjan(int x)
{
	Low[x]=Dfn[x]=++Cnt,Stk[++Top]=x,Ins[x]=1;
	for(int e=Head[x],v;e;e=Edge[e].next)
	{
		if(!Dfn[v=Edge[e].to])
		{
			Tarjan(v);
			checkMin(Low[x],Low[v]);
		}
		else if(Ins[v]) checkMin(Low[x],Dfn[v]);
	}
	if(Dfn[x]==Low[x])
	{
		++Sc;
		while(Stk[Top]!=x)
		{
			Scc[Stk[Top]]=Sc;
			++Sizc[Sc],Ins[Stk[Top]]=0;
			--Top;
		}
		Scc[x]=Sc,++Sizc[Sc];
		Ins[x]=0,--Top;
	}
}
struct Edges
{
	int fr,to,val;ll rec;
}Ed[MAXM];
inline ll calc(int v,int c)
{
	if(!c) return v;
	ll res=0;
	while(v) res+=v,v=v*c/10;
	return res;
}
int Val[MAXN],Dist[MAXN];
bool Vis[MAXN];
inline int Spfa(int st)
{
	std::queue<int>Q;Q.push(st);
	memset(Dist,-0x3f,sizeof(Dist)),Dist[st]=Val[st];
	while(!Q.empty())
	{
		int x=Q.front();Q.pop();
		Vis[x]=0;
		for(int e=Head[x],v;e;e=Edge[e].next)
		{
			v=Edge[e].to;
			if(Dist[v]<Dist[x]+Edge[e].val+Val[v])
			{
				Dist[v]=Dist[x]+Edge[e].val+Val[v];
				if(!Vis[v]) Q.push(v);
			}
		}
	}
	int res=0;
	for(int i=1;i<=Sc;++i) checkMax(res,Dist[i]);
	return res;
}
int main()
{
    // freopen(".in","r",stdin);
    // freopen(".out","w",stdout);
	read(N,M);
	for(int i=1,u,v,w;i<=M;++i)
	{
		long double c;read(u,v,w),scanf("%Lf",&c);
		addEdge(u,v,w);Ed[i]=(Edges){u,v,w,calc(w,10*c)};
		// write(calc(w,c),'\n');
	}
	for(int i=1;i<=N;++i) if(!Dfn[i]) Tarjan(i);
	read(St);
	memset(Head,0,sizeof(Head)),Total=0;
	// for(int i=1;i<=N;++i) write(Scc[i],' ');puts("");
	for(int i=1;i<=M;++i)
	{
		auto e=Ed[i];
		if(Scc[e.fr]==Scc[e.to]) Val[Scc[e.fr]]+=e.rec;
		else addEdge(Scc[e.fr],Scc[e.to],e.val);
		// printf("%d to %d for %d\n",Scc[e.fr],Scc[e.to],e.val);
	}
	write(Spfa(Scc[St]));
	return 0;
}
/*

*/

---

边双连通分量

定义

注意此边双连通分量与之后的点双连通分量都是针对无向图的定义。

边双连通分量指的是一张无向图 去掉所有的桥之后留下来的很多个连通块，每个连通块记为该图的一个边双连通分量。

给一个比较直观的例子：

对于这张图而言，其割边（桥）有两个，一个是 ，一个是 。

那同样的，这张图有三个边双连通分量：

每一个边双连通分量都有一个性质：删除该分量中的任意一条边，该分量依然连通。

Tarjan 求边双

我们考虑将缩点里的 进行改造使其能够帮助我们得到边双。

考虑依然写两个函数为 dfn[] 和 low[] ，表示的信息与缩点中的 相同。

我们同样考虑桥对于其它边而言有的特殊性质。如果我们从结点 通过桥走到结点 ，但这条边 是从 通向 的唯一路径，所以对于当前遍历路径，low[v] 不会被 dfn[u] 所更新。 因为 不可能通过其它的路径走回到 去。

这就是我们判桥的关键，即如果一条边 满足 ，则该边为桥。那接下来的工作就很显然了。

这里介绍两种方法。

缩点栈式

同样的，考虑用缩点里使用 的方法帮助我们得到边双，但需要一些改进。

我首先尝试了一下口胡，后来发现不管怎么提交都是 ，把数据下载之后发现这个点有一个奇妙的特性——自环和重边，容易发现，在边双的定义中，重边不会被判除，而是将其视作非桥边，自环同理，但是在缩点的那个方法中，因为涉及到要像树遍历那样记录 dfs(int x,int last) ，就会直接舍弃重边，导致奇奇妙妙的错误，因此，我们不能判 Ins[x] 和 last ，而是记录当前的 是从边编号 转移而来的。

这样的话，我们使用网络流那种方法来记录每一条边的反边（即 ），然后判断我们是从什么地方转移，从而避免死循环，且我们的 Tarjan(v) 执行判断的是 dfn[v] 是否有值，这样尽管有重边，我们依然能够使得每一个结点至多被遍历一次，从而确保 的时间复杂度为线性。

参考代码

int Dfn[MAXN],Low[MAXN],Stk[MAXN],Cnt,Top;
int Dcc[MAXN],Sizc[MAXN],Dc;
void Tarjan(int x,int last,int le)
{
	Dfn[x]=Low[x]=++Cnt,Stk[++Top]=x;
	for(int e=Head[x],v;e;e=Edge[e].next)
	{
		v=Edge[e].to;
		// if((v=Edge[e].to)==last) continue;
		if(!Dfn[v])
		{
			Tarjan(v,x,e);
			checkMin(Low[x],Low[v]);
		}
		else if(e!=(le^1)) checkMin(Low[x],Dfn[v]);
		if(Low[v]>Dfn[x])
		{
			// write("bridge:",x,' ',v,"\nnow stack:");
			// for(int i=1;i<=Top;++i) write(Stk[i],' ');
			// puts("");
			++Dc;
			while(Stk[Top]!=v)
			{
				Dcc[Stk[Top]]=Dc,++Sizc[Dc];
				--Top;
			}
			Dcc[v]=Dc,++Sizc[Dc],--Top;
		}
	}
}
/*
int main()
{
	for(int x=1;x<=N;++x) if(!Dfn[x])
	{
		Tarjan(x,0,-1);
		if(Top)
		{
			++Dc;
			while(Top)
			{
				Dcc[Stk[Top]]=Dc,++Sizc[Dc];
				--Top;
			}
		}
	}
}
*/

---

二次 dfs 写法

这个写法似乎要更为广泛流传一些，由于我们已经知道的判断桥的方法，那么我们可以通过这个把所有的桥全部标记，然后“删除”这些桥（即判掉），然后再对整张图跑 dfs() ，当然，跑了多少次，就有多少个边双连通分量，即可。

参考代码

int Dfn[MAXN],Low[MAXN],Cnt;
bool Bridge[MAXM<<1];
void Tarjan(int x,int le)
{
	Dfn[x]=Low[x]=++Cnt;
	for(int e=Head[x],v;e;e=Edge[e].next)
	{
		if(!Dfn[(v=Edge[e].to)])
		{
			Tarjan(v,e);
			checkMin(Low[x],Low[v]);
		}
		else if(e!=(le^1)) checkMin(Low[x],Dfn[v]);
		if(Low[v]>Dfn[x]) Bridge[e]=Bridge[e^1]=1;
	}
}
int Dcc[MAXN],Dc;
std::vector<int>Edcc[MAXN];
void dfsBri(int x,int id)
{
	Edcc[id].push_back(x),Dcc[x]=id;
	for(int e=Head[x],v;e;e=Edge[e].next)
	{
		if(Bridge[e]) continue;
		if(!Dcc[(v=Edge[e].to)]) dfsBri(v,id);
	}
}
// 	for(int x=1;x<=N;++x) if(!Dfn[x]) Tarjan(x,-1);
// 	for(int x=1;x<=N;++x) if(!Dcc[x]) dfsBri(x,++Dc);

---

比较

在我看来，二次 dfs 写法会比缩点栈更容易理解一些，因为很直观，而且似乎也很好写一些；从效率上来讲，则缩点栈更优。

例题

待补充。

---

点双连通分量

点双连通分量的定义在与，删去该连通分量里的任意一个结点及其连边，该子图仍然连通，则该子图称为点双连通分量。

将一张无向图的所有割点删去后，每一个连通块与和其直接相连的所有割点为一个点双连通分量，此外，任意两个相连的结点也是一个边双连通分量，还是给出一个直观的例子：

在上图中，一共有两个割点： ，一共有三个点双连通分量：

容易发现， 分别被记录在了两个点双中，因为它们是割点。

但是，割点与点双并不等价，如下图所示：

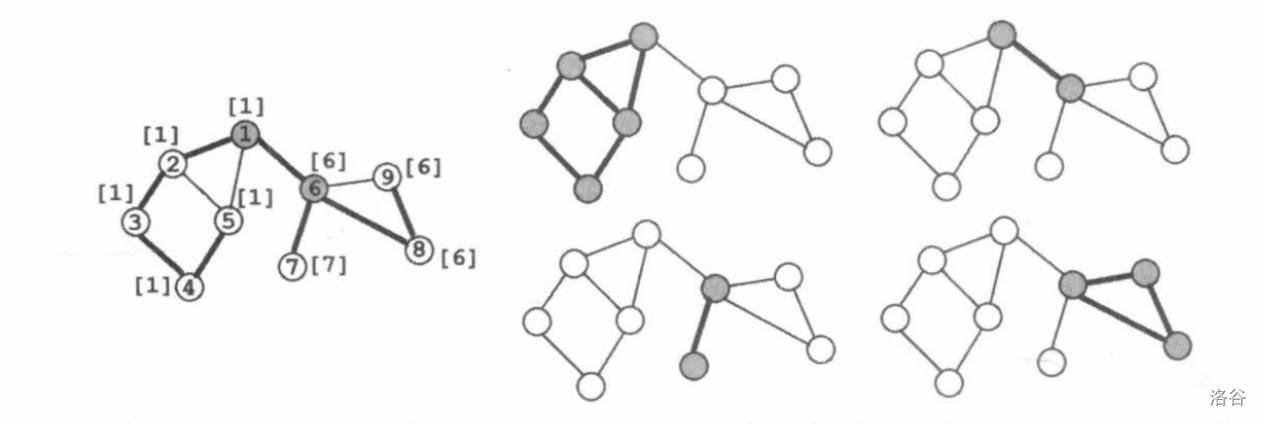
这张图有 个割点，有 个点双。

Tarjan 求点双

我们走老路，还是考虑如何使用 dfn[x],low[x] 来解决这个问题。

与桥类似，如果 是一个割点，那我们的 就不可能通过其它结点走回 之前的结点，那么 low[v] 就不会被 之前的结点所更新，就会满足 的条件，那 就是割点。

然后就显然了。

栈式求点双

由于我们知道每一个结点不止会被包含在一个点双里，所以对于割点，我们需要多次入栈弹栈。

假设当前我们遍历到的结点 是一个割点，那栈中 上的所有结点属于一个点双，我们将其弹出，但我们并不能弹出 ，因为 可能还会属于其它的点双，所以我们只能对 进行特殊处理。

且判栈顶的时候也必须判 而非 。

此外，如果一个点是我们在 dfs 这个连通分量时第一个进入的点，且该连通块真就是个点双，根结点（假定这么称呼）会被误判，这个体现在代码最后一行。

参考代码

int Dfn[MAXN],Low[MAXN],Stk[MAXN],Cnt,Top;
int Dcc[MAXN],Dc;
std::vector<int>Vdcc[MAXN];
void Tarjan(int x,int fa)
{
	Dfn[x]=Low[x]=++Cnt,Stk[++Top]=x;
	int son=0;
	for(int e=Head[x],v;e;e=Edge[e].next)
	{
		if(!Dfn[(v=Edge[e].to)])
		{
			Tarjan(v,x);++son;
			checkMin(Low[x],Low[v]);
			if(Low[v]>=Dfn[x])
			{
				++Dc;	
				while(Stk[Top+1]!=v)
				{
					Vdcc[Dc].push_back(Stk[Top]);
					Dcc[Stk[Top]]=Dc,--Top;
				}
				Dcc[x]=Dc,Vdcc[Dc].push_back(x);
			}
		}
		else if(v!=fa) checkMin(Low[x],Dfn[v]);
	}
	if(!fa&&!son) Vdcc[++Dc].push_back(x);
}
//	for(int x=1;x<=N;++x) if(!Dfn[x]) Tarjan(x,0);

目前好像只有这种方法。

---

例题

求割点

判断割点，也就是求多次在不同点双出现的结点，甚至比求点双简单一些。

AC Code

// ----- Eternally question-----
// Problem: P3388 【模板】割点（割顶）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3388
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// Written by: Eternity
// Time: 2022-12-07 16:08:36
// ----- Endless solution-------
const int MAXN=2e4+10,MAXM=1e5+10;
int N,M;
struct G
{
	int next,to;
}Edge[MAXM<<1];
int Head[MAXN],Total;
inline void addEdge(int u,int v)
{
	Edge[++Total]=(G){Head[u],v};Head[u]=Total;
	Edge[++Total]=(G){Head[v],u};Head[v]=Total;
}
int Dfn[MAXN],Low[MAXN],Cnt;
bool Cut[MAXN];
void Tarjan(int x,int last)
{
	int son=0;
	Dfn[x]=Low[x]=++Cnt;
	for(int e=Head[x],v;e;e=Edge[e].next)
	{
		if(!Dfn[(v=Edge[e].to)])
		{
			Tarjan(v,x);++son;
			checkMin(Low[x],Low[v]);
			if(Low[v]>=Dfn[x]) Cut[x]=1;
		}
		else if(v!=last) checkMin(Low[x],Dfn[v]);
	}
	if(!last&&son<2) Cut[x]=0;
}
std::vector<int>Ct;
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(N,M);
	for(int i=1,u,v;i<=M;++i){ read(u,v);addEdge(u,v); }
	for(int x=1;x<=N;++x) if(!Dfn[x]) Tarjan(x,0);
	for(int x=1;x<=N;++x) if(Cut[x]) Ct.push_back(x);
	write(Ct.size(),'\n');
	for(int x:Ct) write(x,' ');
	return 0;
}
/*

*/

---

待补充。

---

结语

最近 的疫情越来越严重了，或者讲，整个中国，整个世界的疫情都出现了前所未有的严重。听说 已经拉了好几车人，又听说 高三高二都出现了阳性病例，竞赛也已经上了好几天了。

听说新冠已经按普通感冒或者发烧处理了，有些吓人呢。

今天把 一周目打通了，顺便也把这玩意儿写完了，但是又堆了 和 没写，明天又要回归常规了。

日子就这么一天一天过下去吧，不要奢求太多了。

---