Reincarnation

正因为梦易碎，才格外美好。

布尔型广度优先搜索

发表于 更新于 分类于 ，
本文字数： 22k 阅读时长 ≈ 20 分钟

“万物归零，万物始壹。”

更新日志



最近做多项式做得有点悬乎，来学点稍微简单点的。明天 ，准备跑路。



初三回来上 力，本来想着水水，但是还是补一点这个的笔记吧（主要不知道该做啥了。完稿。

0/1 Bfs

考虑下面一个问题：

最短路

给定一个有 个结点， 条边的无向图，给定 ，求从 到 的最短路，保证连通。

数据范围：

容易发现，这就是一个最短路的板子， 的 当然不考虑， 的 估计也会被卡。但 的 大概也不太靠谱。

那怎么做？有没有线性的最短路算法？

注意到一个特殊条件，即边权范围为 ，也就是只有 两种取值方式，有什么用呢？我们要求的是最短路，那我们找到的答案一定是 最多， 最少的一个方案，这样的距离一定是最小的。

我们贪心的考虑取到更多的 ，类似于 的思路，把当前最优解提到队列最前面，因为没有负权，所以这样的思路是正确的。但如果每一次 push 都给出一个排序，那就会多一支 ，我们的时间承受不住。所以，我们直接考虑将 放在队首，将 放在队尾，满足当前结点的贪心思路。用一个双端队列来维护。

0/1 Bfs 的正确性？

考虑维护整个队列都是一个单调递增的，也就是维护一个单调队列。从第一部开始，我们就执行将 边结点放队头， 边结点放队尾，那当这个结点转移结束之后，队列中至多存在路径为 的未转移结点，然后我们又将 结点拿出，同样操作，直到 结点被转移完毕，拿出 结点，这样的话，队列中至多存在路径为 的未转移结点。

所以，当我们当前的转移路径为 ，队列中就至多存在 两种情况，而转移途中也只会产生 两种情况，所以，我们将 放队头， 放队尾，此时整个队列依然是单调递增的。

那我们来分析一下复杂度，每一个结点至多会被枚举一次，每一条边至多会被转移一次，所以最后的时间复杂度为 ，容易发现， 对其的时间复杂度差异就在其使用优先队列的那一支 上。

当然，此处的 其实是一种抽象概念， 可以适用于任意只有两种边权的最短路中。

例题

模板题

题目简介

题目名称：小明的游戏 / /

题目来源：

评测链接 ：https://www.luogu.com.cn/problem/P4554
评测链接 ：https://www.spoj.com/problems/KATHTHI/
评测链接 ：https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=27&page=show_problem&problem=2620

形式化题意：给定一张 的网格图，可以向上下左右四个方向行进，某些代价为 ，某些代价为 ，给定询问 问从 到 的最小代价。

数据范围：

意识到时间复杂度只能做到 ，否则会炸，所以考虑 ，就解决。

参考实现
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
std::deque<Pir>Q;
for(int i=1;i<=N;++i)
	for(int j=1;j<=M;++j) Dist[i][j]=INF,Vis[i][j]=0;
Q.push_back(Pir{sx,sy});
Dist[sx][sy]=0;
while(!Q.empty())
{
	Pir x=Q.front();Q.pop_front();
	if(Vis[x.fir][x.sec]) continue;
	Vis[x.fir][x.sec]=1;
	for(int k=1;k<=4;++k)
	{
		Pir nxt=Pir({x.fir+dx[k],x.sec+dy[k]});
		if(nxt.fir<1||nxt.fir>N||nxt.sec<1||nxt.sec>M) continue;
		int delta=1-(Mp[x.fir][x.sec]==Mp[nxt.fir][nxt.sec]);
		if(Dist[nxt.fir][nxt.sec]>Dist[x.fir][x.sec]+delta)
		{
			Dist[nxt.fir][nxt.sec]=Dist[x.fir][x.sec]+delta;
			if(!delta) Q.push_front(nxt);
			else Q.push_back(nxt);
		}
	}
}

电路维修

题目简介

题目名称：电路维修
题目来源：

评测链接：https://www.acwing.com/problem/content/177

形式化题意：给定一个大小为 的网格图，每一个网格由 / 或 \ 构成，其中 \ 表示左上角和右下角可以互通，/ 表示左下角和右上角可以互通。你可以进行很多次操作使得某一个网格的 / 或者 \ 变成 \ 和 /，问从网格最左上角到最右下角的最少操作次数，多测，无解输出 NO SOLUTION。

形如：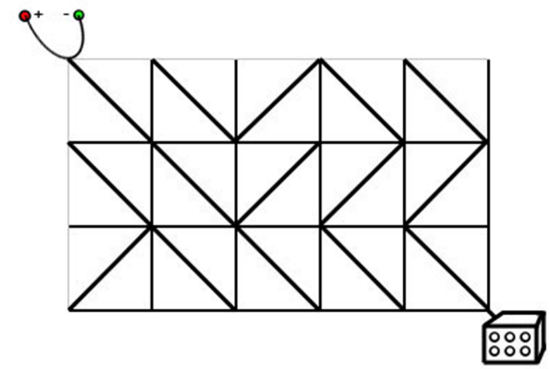
from Acwing

数据范围：

考虑到将网格图抽象为一张有 个结点的图，记第 行第 列的点在图中的编号为 。那么，如果一个网格中为 \，则说明 与 有一条代价为 的无向边。而如果我们对其进行一次操作，则会产生一点代价，使得 和 无代价连通，合并为 和 有一条代价为 的无向边，然后求 到 的最短路。

考虑到图中边权只有 ，可以用 求解，时间复杂度 。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
// ----- Eternally question-----
// Problem: 电路维修
// Contest: AcWing
// URL: https://www.acwing.com/problem/content/177/
// Memory Limit: 64 MB
// Time Limit: 1000 ms
// Written by: Eternity
// Time: 2023-01-16 18:29:24
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ putchar(x?'1':'0'); }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=5e2+10,MAXV=5e5+10,MAXE=1e6+10;
const int INF=0x3f3f3f3f;
int Test,N,M;
char Mp[MAXN][MAXN];
struct G
{
	int next,to,val;
}Edge[MAXE<<1];
int Head[MAXV],Total=1;
inline int getId(int x,int y){ return (x-1)*(M+1)+y;}
inline void addEdge(int u,int v,int w)
{
	Edge[++Total]=(G){Head[u],v,w};Head[u]=Total;
	Edge[++Total]=(G){Head[v],u,w};Head[v]=Total;
}
bool Vis[MAXV];
int Dist[MAXV];
void Bfs()
{
	std::deque<int>Q;
	Q.push_back(1),Dist[1]=0;
	while(!Q.empty())
	{
		int x=Q.front();Q.pop_front();
		if(Vis[x]) continue;
		Vis[x]=1;
		for(int e=Head[x],v;e;e=Edge[e].next)
		{
			v=Edge[e].to;
			if(Dist[v]>Dist[x]+Edge[e].val)
			{
				Dist[v]=Dist[x]+Edge[e].val;
				if(Edge[e].val) Q.push_back(v);
				else Q.push_front(v);
			}
		}
	}
}
inline void init(int n,int m)
{
	Total=1;
	for(int i=1;i<=n*m;++i)
		Dist[i]=INF,Vis[i]=Head[i]=0;
}
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(Test);
	while(Test--)
	{
		read(N,M);
		init(N+1,M+1);
		for(int i=1;i<=N;++i) scanf("%s",Mp[i]+1);
		for(int i=1;i<=N;++i)
			for(int j=1;j<=M;++j)
			{
				int delta=Mp[i][j]=='/';
				addEdge(getId(i,j),getId(i+1,j+1),delta);
				addEdge(getId(i+1,j),getId(i,j+1),delta^1);
			}
		Bfs();
		int res=Dist[getId(N+1,M+1)];
		if(res==INF) puts("NO SOLUTION");
		else write(res,'\n');
	}
	return 0;
}
/*

*/

B. Frog Traveler

题目简介

题目名称：青蛙的旅行
题目来源：

评测链接：https://codeforces.com/problemset/problem/1601/B

一共有 个格子，每个格子有 个参数 ，初始在第 格，每一次可以选择向前跳 格，但当跳到第 格时，会向后退 格（这一步不算次数），求跳到第 格的最小步数以及方案。如果无法到达，输出 -1。

数据范围：

考虑通过建图来解决这个问题。

我们首先将 平移到 ，令 。

对 ，我们建立其镜像点记为 。

  • 对于每一个 ，我们从 向 连边；
  • 对于每一个 ，我们从 向 连边。

都是单向边，这样保证了跳一次和滑一次的行动是对应的。但容易发现，这样的图边数是 的，而我们建图的 为统一区间，所以考虑线段树优化建图。

时间复杂度为 ，空间复杂度玄学，开到了 才过。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
// ----- Eternally question-----
// Problem: Frog Traveler
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF1601B
// Memory Limit: 500 MB
// Time Limit: 2000 ms
// Written by: Eternity
// Time: 2023-01-16 19:51:36
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ putchar(x?'1':'0'); }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=3e5+10,MAXV=4e6+10,MAXE=8e6+10;
const int INF=0x3f3f3f3f;
#define ls(p) Tr[p].lc
#define rs(p) Tr[p].rc
int N,Rt,Idx;
struct St
{
	int lc,rc,id;
}Tr[MAXV<<2];
struct G
{
	int next,to,val;
}Edge[MAXE];
int Head[MAXV],Total=1;
inline void addEdge(int u,int v,int w)
{
	// printf("addEdge:%d to %d\n",u,v);
	Edge[++Total]=(G){Head[u],v,w};Head[u]=Total;
	// Edge[++Total]=(G){Head[v],u,w};Head[v]=Total;
}
void build(int &p,int l,int r)
{
	if(!p) p=++Idx;
	Tr[p].id=p;
	if(l==r) return Tr[p].id=l,void();
	int mid=(l+r)>>1;
	build(ls(p),l,mid),build(rs(p),mid+1,r);
	addEdge(Tr[p].id,Tr[ls(p)].id,0),addEdge(Tr[p].id,Tr[rs(p)].id,0);
}
void addEdge(int p,int x,int ql,int qr,int l,int r,int v)
{
	if(!p||ql>qr) return ;
	if(ql<=l&&r<=qr) return addEdge(x,Tr[p].id,v);
	int mid=(l+r)>>1;
	if(ql<=mid) addEdge(ls(p),x,ql,qr,l,mid,v);
	if(mid<qr) addEdge(rs(p),x,ql,qr,mid+1,r,v);
}
int Dist[MAXV],Prev[MAXV];
void Bfs(int st)
{
	std::deque<int>Q;
	std::memset(Dist,0x3f,sizeof(Dist));
	Q.push_back(st);
	Dist[st]=0;
	while(!Q.empty())
	{
		int x=Q.front();Q.pop_front();
		for(int e=Head[x],v;e;e=Edge[e].next)
		{
			v=Edge[e].to;
			if(Dist[v]>Dist[x]+Edge[e].val)
			{
				Dist[v]=Dist[x]+Edge[e].val,Prev[v]=x;
				if(Edge[e].val) Q.push_back(v);
				else Q.push_front(v);
			}
		}
	}
}
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(N),++N;
	Idx=N<<1;
	build(Rt,1,N);
	for(int i=2,a;i<=N;++i){ read(a);addEdge(Rt,i+N,i-a,i,1,N,1); }
	for(int i=2,b;i<=N;++i){ read(b);addEdge(i,i+b+N,0); }
	Bfs(N<<1);
	int res=Dist[1];
	if(res==INF) puts("-1");
	else
	{
		write(res,'\n');
		std::vector<int>ans;
		for(int s=1;s!=(N*2);s=Prev[s]) ans.push_back(s);
		for(int i=ans.size()-1;~i;--i)
			if(ans[i]<=N) write(ans[i]-1,' ');
	}
	return 0;
}
/*

*/

通信线路

题目简介

题目名称：通信线路
题目来源：

评测链接：https://www.acwing.com/problem/content/342/

形式化题意：给定一张 个结点 条边的无向图，每一条边都有一个权值，定义 的最短路为其一条路径中的边权最大值的最小值，即令 表示一条 到 的一条连通路径，则 的最短路径为 ，你有 次机会可以将一条边的权值赋为 ，求从 到 的最短路。

数据范围：

我们设定现在需要求得的答案为 ，那意味着对于我们任意 的边，一旦我们经过，就会产生一次代价，那我们转换问题：

对于当前阈值 ，我们将 的边权视为 ，反之视为 ，然后进行一次最短路，如果 的最短路小于等于 ，则说明当前答案合法，反之不合法。容易发现， 满足单调性，所以可以进行二分，然后基于特殊边权使用 进行时间复杂度优化。

最后实现：。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
// ----- Eternally question-----
// Problem: 通信线路
// Contest: AcWing
// URL: https://www.acwing.com/problem/content/description/342/
// Memory Limit: 64 MB
// Time Limit: 1000 ms
// Written by: Eternity
// Time: 2023-01-16 21:29:49
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ putchar(x?'1':'0'); }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=1e3+10,MAXM=1e4+10;
const int INF=0x3f3f3f3f;
int N,M,K;
struct G
{
	int next,to,val;
}Edge[MAXM<<1];
int Head[MAXN],Total=1;
inline void addEdge(int u,int v,int w)
{
	Edge[++Total]=(G){Head[u],v,w};Head[u]=Total;
	Edge[++Total]=(G){Head[v],u,w};Head[v]=Total;
}
int Dist[MAXN],MaxK;
void Bfs(int st,int s)
{
	std::memset(Dist,0x3f,sizeof(Dist));
	std::deque<int>Q;
	Q.push_back(st),Dist[st]=0;
	while(!Q.empty())
	{
		int x=Q.front();Q.pop_front();
		for(int e=Head[x],v;e;e=Edge[e].next)
		{
			v=Edge[e].to;
			int delta=(Edge[e].val>s);
			if(Dist[v]>Dist[x]+delta)
			{
				Dist[v]=Dist[x]+delta;
				if(delta) Q.push_back(v);
				else Q.push_front(v);
			}
		}
	}
}
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(N,M,K);
	for(int i=1,u,v,w;i<=M;++i){ read(u,v,w);addEdge(u,v,w);checkMax(MaxK,w); }
	int l=0,r=MaxK,res=r;
	Bfs(1,MaxK);
	if(Dist[N]==INF) return puts("-1"),0;
	while(l<=r)
	{
		int mid=(l+r)>>1;
		Bfs(1,mid);
		if(Dist[N]>K) l=mid+1;
		else r=mid-1,res=mid;
	}
	write(res);
	return 0;
}
/*

*/

E. Cactus Wall

题目简介

题目名称：

题目来源：

评测链接：https://codeforces.com/problemset/problem/1749/E

形式化题意：给定一张 的网格图，其中一些格子为 # 表示障碍，障碍不可通过，且不存在任意两个障碍相邻，问原图的基础上，是否存在一种放置障碍的方案使得第 行和第 列不连通。多测，输出方案。

数据范围：

假设我们现在已经得到了最后的障碍图，如果我们从第 行出发到第 行，假设走普通路不记录代价，走到障碍记录代价为 ，则该最短路的最小代价必然 ，这就是我们需要的状态。

那我们再考虑一下，如果我们反转代价，当走到障碍时不记录代价，相反代价为 ，那对于最终状态，从第 列到第 列的最短路为 时，则不连通，也就是我们已经有了一条穿越了一整行的全部由 # 构成的最短路，也就是一条屏障。

考虑建图（ 也不可能用邻接矩阵存吧），从第 列到第 列跑 ，障碍代价为 ，反之为 ，每到一个结点判断其与原图的矛盾性（也就是这个结点四周是否已经存在障碍），然后记录转移前驱即可。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
// ----- Eternally question-----
// Problem: E. Cactus Wall
// Contest: Codeforces - Educational Codeforces Round 138 (Rated for Div. 2)
// URL: https://codeforces.com/problemset/problem/1749/E
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// Written by: Eternity
// Time: 2023-01-25 09:58:27
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ putchar(x?'1':'0'); }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXN=4e5+10,MAXM=2e6+10;
const int INF=0x3f3f3f3f;
const int dx[]={0,1,-1,0,0,1,1,-1,-1};
const int dy[]={0,0,0,1,-1,1,-1,1,-1};
int Test,N,M;
struct G
{
	int next,to;
}Edge[MAXM<<1];
int Head[MAXN],Total;
inline void addEdge(int u,int v)
{
	Edge[++Total]=(G){Head[u],v};Head[u]=Total;
	Edge[++Total]=(G){Head[v],u};Head[v]=Total;
}
inline int getId(int x,int y)
{ return (x-1)*M+y; }
int Dist[MAXN],Prev[MAXN];
bool Vis[MAXN];
char Mp[MAXN];
inline bool around(int v)
{
	int y=(v-1)%M+1;
	int x=(v-y)/M+1;
	for(int k=1;k<=4;++k)
	{
		int nx=x+dx[k],ny=y+dy[k];
		if(nx<1||nx>N||ny<1||ny>M) continue;
		if(Mp[getId(nx,ny)]=='#') return 1;
	}
	return 0;
}
inline void Bfs()
{
	std::deque<int>Q;
	for(int i=1;i<=N;++i)
	{
		if(around(getId(i,1))) continue;
		if(Mp[getId(i,1)]=='.') Q.push_back(getId(i,1)),Dist[getId(i,1)]=1;
		else Q.push_front(getId(i,1)),Dist[getId(i,1)]=0;
	}
	while(!Q.empty())
	{
		int u=Q.front();Q.pop_front();
		if(Vis[u]) continue;
		Vis[u]=1;
		for(int e=Head[u],v;e;e=Edge[e].next)
		{
			v=Edge[e].to;
			if(around(v)) continue;
			int delta=(Mp[v]=='.');
			if(Dist[v]>Dist[u]+delta)
			{
				Dist[v]=Dist[u]+delta,Prev[v]=u;
				if(delta) Q.push_back(v);
				else Q.push_front(v);
			}
		}
	}
}
int minpos,minans;
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(Test);
	while(Test--)
	{
		read(N,M);
		for(int i=1;i<=N*M;++i)
		{
			char c=getchar();
			Dist[i]=INF,Vis[i]=0,Prev[i]=0;
			while(c!='.'&&c!='#') c=getchar();
			Mp[i]=c;Head[i]=0;
		}
		Total=0;
		for(int i=1;i<=N;++i)
			for(int j=1;j<=M;++j)
				for(int k=5;k<=8;++k)
				{
					int nx=i+dx[k],ny=j+dy[k];
					if(nx<1||nx>N||ny<1||ny>M) continue;
					addEdge(getId(i,j),getId(nx,ny));
				}
		Bfs();
		minans=INF;
		for(int i=1;i<=N;++i)
			if(checkMin(minans,Dist[getId(i,M)])) minpos=getId(i,M);
		if(minans==INF){ puts("NO");continue; }
		for(int x=minpos;x;x=Prev[x]) Mp[x]='#';
		puts("YES");
		for(int i=1;i<=N;++i,puts(""))
			for(int j=1;j<=M;++j) write(Mp[getId(i,j)]);
	}
	return 0;
}
/*

*/

D - Wizard in Maze

题目简介

题目名称：

题目来源：

评测链接：https://atcoder.jp/contests/abc176/tasks/abc176_d

形式化题意：给定一张 的网格图，其中有一些点为障碍，起点为 ，可以花费代价 从 到 中任意不为障碍的点（），也可以不花费代价走四连通，求到达 的最小代价。

数据范围：

建图，对于四连通连代价为 的双向边，对于魔法范围连代价为 的双向边，跑 即可。

点数 ，边数 ，开 1e7 是可以过的。

AC Code
 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
// ----- Eternally question-----
// Problem: D - Wizard in Maze
// Contest: AtCoder - AtCoder Beginner Contest 176
// URL: https://atcoder.jp/contests/abc176/tasks/abc176_d
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
// Written by: Eternity
// Time: 2023-01-25 10:12:07
// ----- Endless solution-------

#include<bits/stdc++.h>
#define re register
typedef long long ll;
template<class T>
inline void read(T &x)
{
	x=0;
	char ch=getchar(),t=0;
	while(ch<'0'||ch>'9') t|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1){ read(x),read(x1...); }
template<class T>
inline void write(T x)
{
	if(x<0) putchar('-'),x=-x;
	if(x>9) write(x/10);
	putchar(x%10+'0');
}
template<>
inline void write(bool x){ putchar(x?'1':'0'); }
template<>
inline void write(char c){ putchar(c); }
template<>
inline void write(char *s){ while(*s!='\0') putchar(*s++); }
template<>
inline void write(const char *s){ while(*s!='\0') putchar(*s++); }
template<class T,class ...T1>
inline void write(T x,T1 ...x1){ write(x),write(x1...); }
template<class T>
inline bool checkMax(T &x,T y){ return x<y?x=y,1:0; }
template<class T>
inline bool checkMin(T &x,T y){ return x>y?x=y,1:0; }
const int MAXP=1e3+10,MAXN=2e6+10,MAXM=1e7+10;
const int INF=0x3f3f3f3f;
const int dx[]={0,1,-1,0,0};
const int dy[]={0,0,0,1,-1};
int N,M,Sx,Sy,Ex,Ey;
char Mp[MAXP][MAXP];
inline int getId(int x,int y)
{ return (x-1)*M+y; }
struct G
{
	int next,to,val;
}Edge[MAXM<<1];
int Head[MAXN],Total;
inline void addEdge(int u,int v,int w)
{
	Edge[++Total]=(G){Head[u],v,w};Head[u]=Total;
	Edge[++Total]=(G){Head[v],u,w};Head[v]=Total;
}
int Dist[MAXN];
bool Vis[MAXN];
inline void Bfs(int st,int ed)
{
	std::deque<int>Q;
	std::memset(Dist,0x3f,sizeof(Dist));
	Dist[st]=0,Q.push_back(st);
	while(!Q.empty())
	{
		int u=Q.front();Q.pop_front();
		if(Vis[u]) continue;
		Vis[u]=1;
		if(u==ed) return ;
		for(int e=Head[u],v;e;e=Edge[e].next)
		{
			v=Edge[e].to;
			if(Dist[v]>Dist[u]+Edge[e].val)
			{
				Dist[v]=Dist[u]+Edge[e].val;
				if(Edge[e].val) Q.push_back(v);
				else Q.push_front(v);
			}
		}
	}
}
int main()
{
	// freopen(".in","r",stdin);
	// freopen(".out","w",stdout);
	read(N,M,Sx,Sy,Ex,Ey);
	for(int i=1;i<=N;++i) scanf("%s",Mp[i]+1);
	for(int i=1;i<=N;++i)
		for(int j=1;j<=M;++j)
		{
			if(Mp[i][j]=='#') continue;
			for(int k=1;k<=4;++k)
			{
				int nx=i+dx[k],ny=j+dy[k];
				if(nx<1||nx>N||ny<1||ny>M) continue;
				if(Mp[nx][ny]=='.') addEdge(getId(i,j),getId(nx,ny),0);
			}
		}
	for(int i=1;i<=N;++i)
		for(int j=1;j<=M;++j) if(Mp[i][j]=='.')
			for(int l=-2;l<=2;++l)
				for(int r=-2;r<=2;++r)
				{
					if(i+l<1||i+l>N||j+r<1||j+r>M) continue;
					if(Mp[i+l][j+r]=='.') addEdge(getId(i,j),getId(i+l,j+r),1);
				}
	Bfs(getId(Sx,Sy),getId(Ex,Ey));
	write(Dist[getId(Ex,Ey)]==INF?-1:Dist[getId(Ex,Ey)]);
	return 0;
}
/*

*/
相关文章