数学高考题选做

“没事，命运如此。”我不再为此感到悲伤，因为他会为我的离开而流泪，我会为他的成功而欢呼。

代数

Problem I

存在函数 的定义域为 ，有：

$$f(x)= \begin{cases} \frac{1}{2}x(2-x)&,x\in(0,1)\\ \lambda f(\frac{x}{2})&,x\geq 1 \end{cases}$$

其中 ，如果 ，，求 的取值范围。

解答

简单地画一下图，发现 后面的部分是一个倍增分块，对于 ，就是将 部分横向拉长一倍后乘上一个 。

设 ，有 。

使用反证法，设 存在，也就有 ，其中 。

我们对式子进行化简：

$$\begin{align} \lambda^k\times\frac{1}{2}\times\frac{x}{2^k}\times\left(2-\frac{x}{2^k}\right)&=\nonumber x \\ \left(\frac{\lambda}{2}\right)^k\left(1-\frac{x}{2^{k+1}} \right)&=1\nonumber \\ 1-\frac{x}{2^{k+1}}&=\nonumber\left(\frac{2}{\lambda}\right)^k \\ \frac{x}{2^{k+1}}&=\nonumber 1-\left(\frac{2}{\lambda}\right)^k \end{align}$$

因为 ，所以有：

$$\begin{align} 1-\left(\frac{2}{\lambda}\right)^k&\in\nonumber\left[\frac{1}{4},\frac{1}{2}\right)\\ \left(\frac{2}{\lambda}\right)^k&\in\nonumber \left(\frac{1}{2},\frac{3}{4}\right] \end{align}$$

设 ，有 ，此时 。

解得 ，所以 。

---

Problem II

已知 ，下列选项中正确的有：

1. 单调递增；
2. ，那么方程 至多有三个解；
3. 若 没有过 的切线，则 。
4. 若正项等比数列 满足 ，则 。

解答

首先对 求导得到：

$$f'(x)=1+\frac{1}{x^2}-\frac{2}{x}$$

化简得 。所以 恒成立， 单调递增。

对 进行求导得：

$$[f'(x)]'=-\frac{2}{x^3}+\frac{2}{x^2}=\frac{2}{x^2}\left( 1-\frac{1}{x} \right)$$

当 时，，而 在 上单增，在 单减，而 在 时单减，在 时单增。

记录 ，那么对 求导得：

$$g'(x)=f'(x)-a$$

对 求导得：

$$[g'(x)]'=[f'(x)]'$$

仅存在一个零点 ，那么 有 个单调区间，至多存在 个零点，所以 至多存在 个单调区间，也就至多存在 个零点，所以构造出至多 个交点。

不存在过 的切线。

，所以 ，假设 ，那么对于 ，有 ，即 。

显然，，所以 成立。

而 单调递增，所以当 时，，求和也小于 ，反之亦然。

---

Problem III

如果对于所有的 有 无解，则 的取值范围。

解答

考虑使用辅助角公式，得到：

$$x\sin x+\cos x=\sin(x+\arcsin\frac{1}{x})\sqrt{1+x^2}$$

所以得到：

$$x\sin x+\cos x\leq \sqrt{1+x^2}$$

那么有 ，然后我们来考虑剩余的部分。设 的情况，其中：

$$\begin{cases} \sin\varphi=\frac{1}{\sqrt{x^2+1}}\\ \cos\varphi=\frac{x}{\sqrt{x^2+1}}\\ \end{cases}$$

若 。

$$\begin{align} x&=\nonumber\frac{\pi}{2}-\varphi\\ \tan x&=\nonumber\tan\left(\frac{\pi}{2}-\varphi\right)\\ \tan x&=\nonumber\frac{1}{\tan\varphi}\\ \tan x&=\nonumber x \end{align}$$

所以有解，得到 。

合一公式/辅助角公式

$$a\sin x+b\cos x=\sqrt{a^2+b^2}\sin(x+\varphi),\tan\varphi=\frac{b}{a}$$

我们选择代几综合的方法来证明：设一个直角三角形的两条直角边分别是 ，那其斜边为 ，也就有：

$$\begin{align} \sin a&=\nonumber \frac{a}{\sqrt{a^2+b^2}}\\ \sin b&=\nonumber \frac{b}{\sqrt{a^2+b^2}}=\cos a \end{align}$$

那么就有：

$$\begin{align} a\sin x+b\cos x&=\nonumber \sqrt{a^2+b^2}\left( \sin x\cdot\frac{a}{\sqrt{a^2+b^2}}+\cos x\cdot\frac{b}{\sqrt{a^2+b^2}} \right) \\&=\nonumber \sqrt{a^2+b^2}\left( \sin x\cdot \cos b+\cos x\cdot \sin b \right) \\&=\nonumber \sqrt{a^2+b^2}\sin(x+\varphi),\tan\varphi=\frac{b}{a} \end{align}$$

同理，可以证明出：

$$a\sin x\pm b\cos x=\sqrt{a^2+b^2}\sin(x\pm\varphi)$$

---

Problem IV

已知实数 满足 ，求 的取值范围。

解答

考虑因为两个式子都是轮换式，所以设 进行换元：

$$\begin{align} x^2+y^2-xy&=\nonumber (a+b)^2+(a-b)^2-(a+b)(a-b) \\&=\nonumber a^2+3b^2=1 \end{align}$$

所以可以得到：，将 消掉代入求解式：

$$\begin{align} x^2+y^2+x+y&=\nonumber (a+b)^2+(a-b)^2+(a+b)+(a-b) \\&=\nonumber 2a^2+2b^2+2a \\&=\nonumber 2a^2+2(\frac{1}{3}-\frac{1}{3}a^2)+2a \\&=\nonumber \frac{4}{3}a^2+2a+\frac{2}{3} \\&=\nonumber \frac{4}{3}(a^2+\frac{3}{2}a+\frac{1}{2}) \\&=\nonumber \frac{4}{3}\left[ (a+\frac{3}{4})^2-\frac{1}{16} \right] \\&=\nonumber \frac{4}{3}(a+\frac{3}{4})^2-\frac{1}{12} \end{align}$$

通过上述式子，可以得到：

$$\begin{cases} a^2\geq 0\\ \frac{1}{3}-\frac{1}{3}a^2\geq 0 \end{cases}$$

解出 ，所以取值范围：。

---

解析几何

Problem I

双曲线 与抛物线 有 个交点，他们共圆，求这个圆的半径。

解答一

将其视作二元二次方程组：

$$\begin{cases} x^2-y^2=1&(1)\\ x^2=4y&(2) \end{cases}$$

用 得到 ，组合化简得到：

$$(x-0)^2+(y-4)^2=15$$

那么满足 方程的二元组都在以 为圆心，半径 的圆上。

解答二

脑袋笨，太久没接触过常规了，复建来做这道题，只会一些稍微复杂的方法。

考虑用几何表示，得到下图：

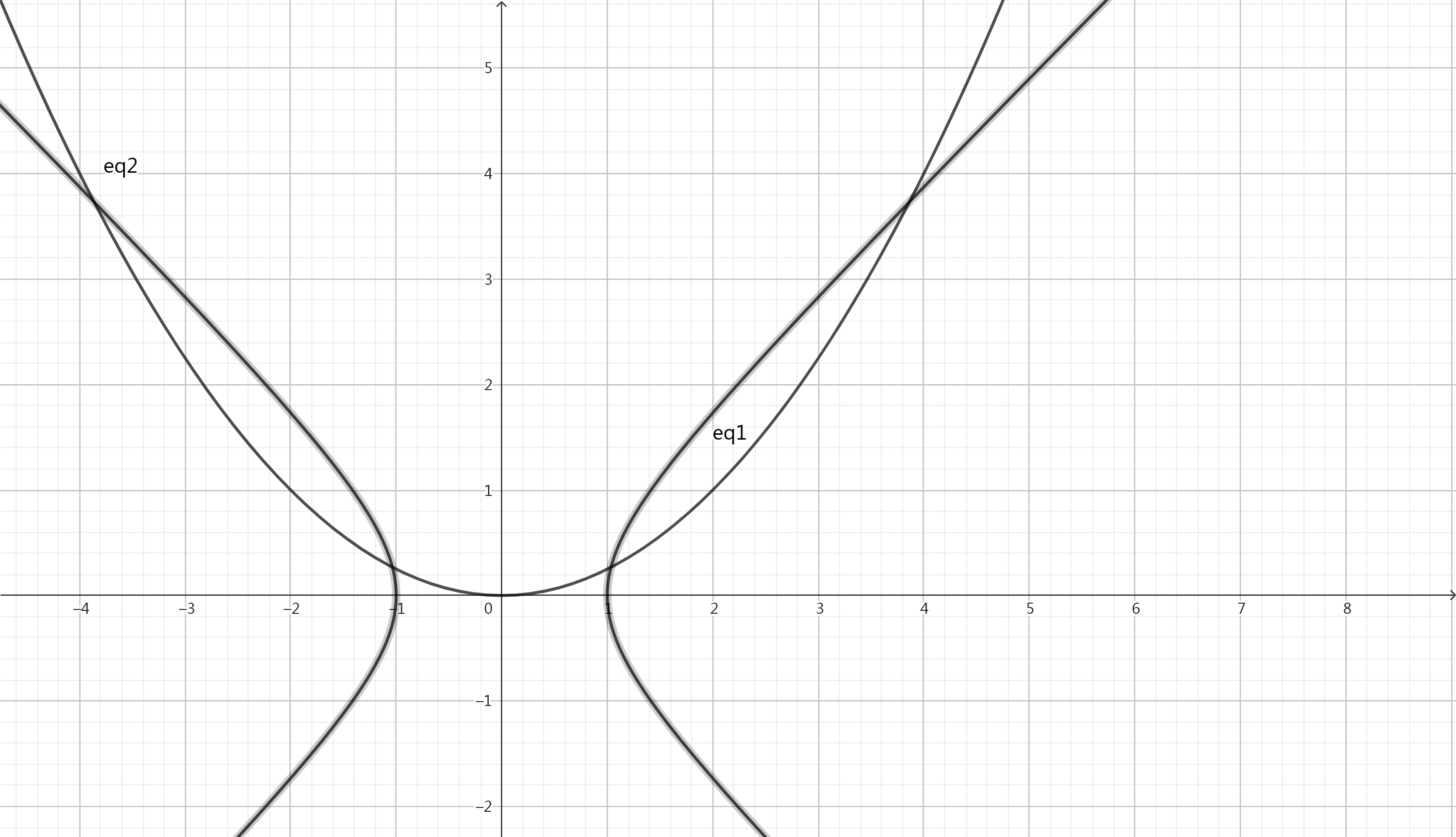
容易发现这四个交点是关于 轴对称的，且有 ，所以此时我们只考虑第一象限。

将 代入双曲线得到：，解得：

$$\begin{cases} y_1=2+\sqrt 3\\ y_2=2-\sqrt 3 \end{cases}$$

然后代回 得 ，也就解得：

$$\begin{align} x^2&=\nonumber 2(\sqrt 3\pm 1)^2\\ x&=\nonumber \pm\sqrt 2(\sqrt 3\pm 1) \end{align}$$

但前文提到我们只需要用到第一象限的点，所以解得 和 。

由圆的定义可以知道，圆心一定在 轴上，且过这两点的中垂线，所以求得过这两点的直线：，那么其中垂线就是：

$$\sqrt 2x+\sqrt 3y-4\sqrt 3=0$$

解得圆心为 ，然后任取一点使用距离公式可以得到半径为 。思维量小，计算量略大。

---

Problem II

被数学竞赛薄纱了。

给定双曲线 ，在 中存在一个动点 ，连接 交 于另一点 ，并连接 交 于另一点 ，求 的取值范围。

解答

设 ，容易得知 ，所以斜率一定存在，设 的斜率式：

$$PA:y=\frac{y_0-1}{x_0}x+1$$

联立 可以得到方程：

$$\begin{align} x^2-\left(\frac{(y_0-1)x}{x_0}+1\right)^2&=\nonumber 1 \\ (1-\left(\frac{y_0-1}{x_0}\right)^2)x^2-\frac{2(y_0-1)}{x_0}x-2&=\nonumber 0 \end{align}$$

或者我们用一种更简单的方式：，得到：

$$(1-k^2)x^2-2kx-2=0$$

当 时，解出 ，所以此时 与 无法相交在另一点。

所以有 ，我们套用韦达定理：

$$\begin{cases} x_0+x_Q=\frac{2k}{1-k^2}\\ x_0\cdot x_Q=\frac{2}{k^2-1} \end{cases}$$

我们同理得到：，联立得到：

$$\begin{cases} x_Q+x_R=\frac{2k_2}{k_2^2-1}\\ x_Q\cdot x_R=\frac{2}{k_2^2-1} \end{cases}$$

所以我们可以得到：

$$\begin{cases} x_R-x_0=\frac{2(k+k_2)kk_2}{(k^2-1)(k_2^2-1)}\\ \frac{x_R}{x_0}=\frac{k^2-1}{k_2^2-1} \end{cases}$$

现在我们尝试用 表示 ，得到：

$$\begin{align} x_Q&=\nonumber\frac{2}{(k^2-1)x_0} \\&=\nonumber \frac{2}{((\frac{(y_0-1)}{x_0})^2-1)x_0} \\&=\nonumber \frac{2}{\frac{y_0^2-x_0^2-2y_0+1}{x_0}} \\&=\nonumber \frac{2}{-\frac{2y_0}{x_0}} \\&=\nonumber -\frac{x_0}{y_0} \end{align}$$

所以我们得到 。那现在我们同样通过 得到 ：

$$\begin{align} x_R&=\nonumber \frac{2}{(k_2^2-1)x_Q} \\&=\nonumber \frac{2}{((\frac{(y_Q-1)}{x_Q})^2-1)x_Q} \\&=\nonumber\cdots \end{align}$$

然后你发现两次式子是对称的。所以有 ，然后换元得到 。

天哪，怎么会如此巧妙！你发现 实际上是关于 轴对称的，所以 。所以 。而有 ，所以不能取 ，得到最后答案：

$$|PR|\in(2,2\sqrt 2)\cup(2\sqrt 2,+\infty)$$

---

Problem III

平面中有 个向量 ，已知 ，求 的取值范围。

解答

设 ，那么得到：，尝试化简式子：

$$\begin{align} (\vec a+\vec c)^2&=\nonumber (\vec z+\vec c)^2 \\ (\vec a)^2+(\vec c)^2+2\vec a\cdot\vec c&=\nonumber (\vec z)^2+(\vec c)^2+2\vec z\cdot\vec c \\ 2(\vec z-\vec a)\vec c&=\nonumber (\vec a)^2-(\vec z)^2 \end{align}$$

记 ，那么我们继续化简：

$$\begin{align} 2|\vec c|\cdot|\vec z-\vec a|\cos\theta&=\nonumber |\vec a|^2-|\vec z|^2 \\ |\vec c|&=\nonumber \frac{|\vec a|^2-|\vec z|^2}{2|\vec z-\vec a|\cos\theta} \\&=\nonumber \frac{|\vec a|^2-|\vec a|^2-|\vec b|^2-2\vec a\cdot\vec b}{2|\vec b|\cos\theta} \\&=\nonumber \frac{|\vec b|^2+2\vec a\cdot\vec b}{2\sqrt 3\cos\theta} \end{align}$$

显然 ，所以得到 。

---