神经网络入门

Function describes the world.

联结主义

一切问题都可以用函数进行表示，这里的函数是广义上的函数，即 中的 不一定只是数，也可以是字符，图像等等。

而 AI 的作用就是通过 的数据集构造拟合函数。

最简单的拟合就是线性拟合，也就是高中学过的线性回归 ，但这样描述并不完全正确，更具体来讲，线性函数能够描述的问题极其有限。

激活函数

所以我们使 作为某一个非线性函数的嵌套，即

$$f(x)=g(wx+b)$$

这里的 称为激活函数，一般是固定的，如

1. 函数：，可以将 转化为 。
2. 函数： 可以解决梯度消失的问题。
3. 函数：，归一化指数函数，映射为一个总和为 的概率分布向量。

神经元与神经网络

当然，输入值不一定会有一个，输出值也不一定只有一个，激活函数也不止一个，所以我们可以将其表示为：

$$f(x_1,x_2,\dots,x_k)=g_1(g_2(\dots g_m(w_1x_1+w_2x_2+\dots+b)))$$

其中 被称为输入层（Input Layer）， 被称为输出层（Output Layer）。

加入我们提取其中某个激活函数，将其视为 ，将一步转化拆分为多步转化，那么中间得到的过渡态称之为隐藏层（Hidden Layer）。所有的层都被视作为一个神经元。

神经元即转化关系组成神经网络。从一个输入层到输出层的转化称为一次前向传播（Forward）。

神经网络大多都是多层感知机（MLP，Multilayer Perceptron）。

拟合与损失函数

那么，如何得到所有的 就是我们通过计算机需要得到的东西。然后如何评判构造函数的好坏，我们在高中数学里也已经学过了，那就是计算残差。

$$L=\sum_{i=1}^{N}\mid y_i-\hat y_i\mid$$

然后你也知道绝对值不甚美观，所以我们提出了均方误差（MSE）的概念：

$$L(w,b)=\frac{1}{N}\sum_{i=1}^{N}(y_i-\hat y_i)^2$$

所以，越优秀的拟合函数，意味着 的值越小。所以，我们需要通过一定的调整使 接近其极小值，也就是求 的极值，使 。

反向传播

我们可以对 取一组初始值，并计算当前的 ，并在进行调整后查看其对 的影响来决定之后是将 加大还是减小，加大多少又减小多少。

也就是

$$\begin{align} w'=w-\eta\frac{\partial L(w,b)}{\partial w}\\ b'=b-\eta\frac{\partial L(w,b)}{\partial b} \end{align}$$

这里的 就是学习率（Learning Rate），偏导数构成的向量就称为梯度，变化 的过程就称为梯度下降。

直接对复合函数求偏导是极其困难的，但是我们会求 的偏导，激活函数又是固定的，所以我们考虑分部求导，也就是对于一个过程：

$$x\rightarrow a\rightarrow \hat y\rightarrow L$$

我们可以通过：

$$\frac{\partial L}{\partial x}=\frac{\partial a}{\partial x}\cdot\frac{\partial \hat y}{\partial a}\cdot\frac{\partial L}{\partial\hat y}$$

然后你会发现 就是最后一层隐藏层的参数更新，所以我们直接从后往前进行更新，这个过程称为反向传播，每一轮称之为训练。

训练调整

鲁棒性

如果训练出的模型仅对训练数据具有极强的拟合，而在处理非训练数据时表现很烂，这意味着这个模型陷入了过拟合。反之，如果模型对任何数据都有一定拟合但表现都不尽人意，这意味着这个模型欠拟合。

这种模型的拟合能力，官方名为鲁棒性（Robustness），指一个系统、模型或算法在面对干扰、异常输入或不确定性因素时，仍能维持核心功能稳定运行的能力。

模型调整

数据增强

我们可以通过对训练数据进行一定的处理或增加训练数据来增强鲁棒性，如对于图像训练集，我们可以通过翻转，反色，增噪等方式扩充训练集，这种方式称为数据增强。

正则化

在多数情况下，过拟合的出现源于某几个参数的野蛮生长，即存在 在调整过程中不断增长导致这一维的 对整体数据的影响极大。所以我们构造一个新的损失函数：

$$\begin{align} L1=L+\lambda\sum_{i=1}^{N}|\omega_i|\\ L2=L+\lambda\sum_{i=1}^{N}{\omega_i}^2 \end{align}$$

我们将 加到损失函数的计算中，从此确保 的极差不会很大。这个过程称为正则化，添加的关于 和的那一项被称为惩罚项， 是正则化系数， 分别是 L1 正则化和 L2 正则化。

和 都属于训练模型的超参数。

Dropout

在每一轮训练中随机无视一部分参数。

---

卷积神经网络，CNN

对于层与层之间，设 ，我们用矩阵形式将其表示出：

$$\begin{pmatrix} y_1 \\ y_2 \end{pmatrix} = \begin{pmatrix} w_{1,1} & w_{1,2} & w_{1,3} \\ w_{2,1} & w_{2,2} & w_{2,3} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} +\begin{pmatrix} b_1 \\ b_2 \end{pmatrix}$$

记为：

$$Y=WX+b$$

我们将神经网络中的第 层记为 ，输入层记为 ，那么通用转移过程即：

$$\alpha^{[L]}=W^{[L]}\alpha^{[L-1]}+b^{[L]}$$

层与卷积

如果 都需要所有 进行转移，也就是由 构成的有向图为完全图，则这个层被称为全连接层（Fully Connected）。

所以说，如果神经网络里所有层都是全连接层，则每一次训练的是时空复杂度达到 ，这是不可控的。因此，我们引入卷积。

对于矩阵 ，卷积操作定义为：

$$A\ast B= \begin{pmatrix} a_{1,1}\times b_{1,1} & \cdots & a_{1,m}\times b_{1,m}\\ \vdots & \ddots & \vdots \\ a_{n,1}\times b_{n,1} & \cdots & a_{n,m}\times b_{n,m} \end{pmatrix}$$

简单说就是对应位置乘积。

所以，在图像处理神经网络中，如果我们将分辨率为 图像在某一个层转化为 个 矩阵，并构造一个固定矩阵 ，使这一层的转移为：

$$\alpha^{[L]}=\alpha^{[L-1]}\ast V$$

那么这一层就被称为卷积层（Conv）， 被称为卷积核，卷积核长什么样子取决于需要什么用处，如图像锐化，图像浮雕等等，在深度学习中，卷积核属于参数，是需要训练过程中进行计算的。

因此，我们可以写出卷积神经网络（CNN）的基本架构：

$$\operatorname{Input}\rightarrow\cdots\rightarrow\operatorname{Conv}\rightarrow\cdots\rightarrow\operatorname{FC}\rightarrow\cdots\rightarrow\operatorname{Output}$$

CNN 一般用于图像处理。

感受野（Receptive Field）

在卷积神经网络中,感受野（Receptive Field）是指特征图上的某个点能看到的输入图像的区域,即特征图上的点是由输入图像中感受野大小区域的计算得到的。神经元感受野的值越大表示其能接触到的原始图像范围就越大，也意味着它可能蕴含更为全局，语义层次更高的特征；相反，值越小则表示其所包含的特征越趋向局部和细节。

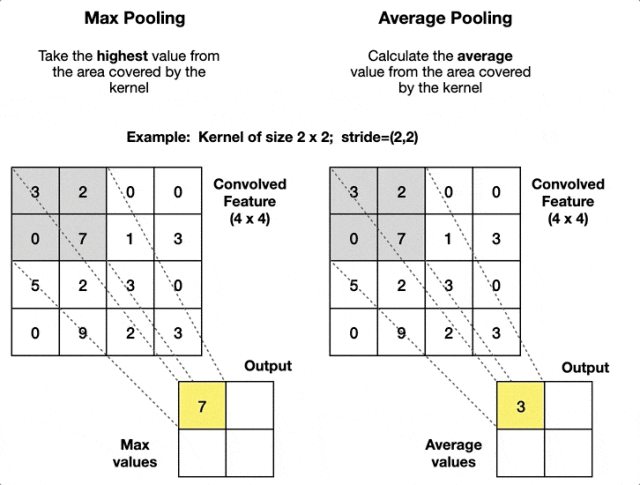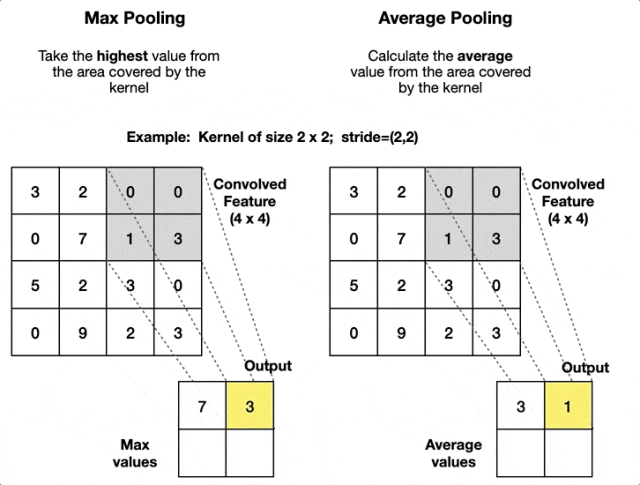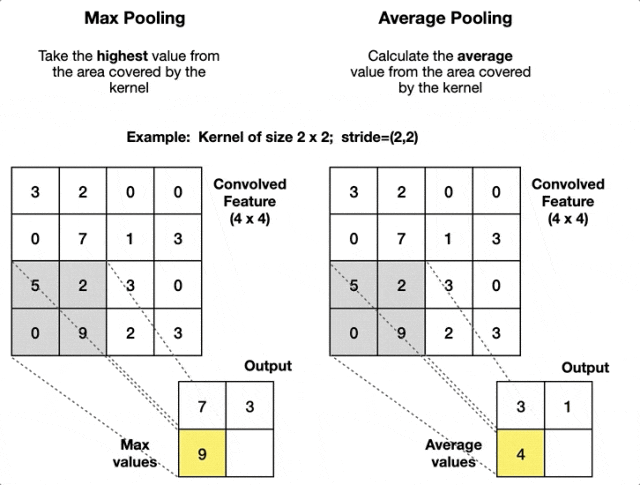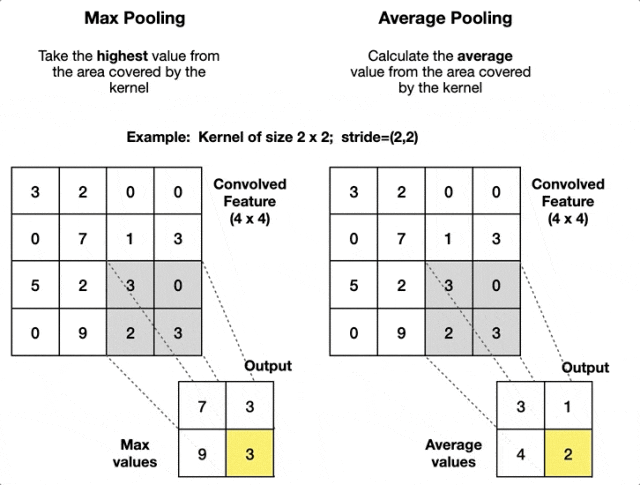
池化

池化是卷积神经网络中的一种下采样操作。它通过定义一个空间邻域（通常为矩形区域），并对该邻域内的特征进行统计处理（如取最大值、平均值等），从而生成新的特征图。池化操作通常紧随卷积层之后。

• 最大值池化：在定义的池化窗口内，选取所有元素中的最大值，并将该最大值作为池化结果输出到下一层特征图的对应位置。
• 平均池化：在定义的池化窗口（如 等）内，计算所有元素的平均值，并将该平均值作为池化结果输出到下一层特征图的对应位置。

池化的重要参数是窗口大小和步长，前者决定操作的区域大小，后者决定滑动距离。

---

循环神经网络，RNN

在处理自然语言的模型中，将文字转化为向量并不容易，如果每一个字都作为一个单位向量，那么所有向量正交，且万维向量毫无意义，计算量巨大，这种独热编码（One Hot）并不优秀。

Word2Vec

我们将所有词向量限制在一个 维空间中，并要求语义相近的词语对应的词向量距离更小。

Word2Vec 基于假设“在文本中，词语距离越近，相似度越高”，我们首先知道这是不完全正确的，但是具有一定拟合性。通过 CBOW（上下文词推测中心词）和 skip-gram（中心词推测上下文词）两种方式进行训练可以得到一个词库的词向量。

当然，Word2Vec 的局限性很大，首先也是最重要的就是其无法处理多义词，并且其上下文窗口（即规定上 个中的这个 ）长度有限使其无法考虑全局文本，也无法做到对于语序的严格要求。

词嵌入（Embedding）

将所有词向量组成一个 的矩阵（ 为词库大小），称为嵌入矩阵。词向量所在的空间称为潜空间。在考虑向量的相似性时，可以用到点积或余弦相似度，也可以通过特殊降维方式使其可视化。

循环神经网络

如果输入层包含整个句子，那么输入层大小就会变成 ，时空复杂度里包含 都是不行的，这样的计算强度极大。

所以考虑每一次传入只传入一个词，我们将第 个词记为 ，其转移记为：

$$X^{\langle i\rangle}\rightarrow g(WX^{\langle i\rangle}+b)$$

为了考虑词语在句子中的顺序关系，我们让转移具有一定前缀性，即将 的转移记为隐藏层 ，并让 参与后续转移：

$$X^{\langle i+1\rangle}\rightarrow g\big(W_{i+1,x}X^{\langle i+1\rangle}+W_{i+1,h}h^{\langle i\rangle})+b_{i+1}\big)$$

令 的转移变为：

$$X^{\langle i\rangle}\rightarrow g(W_{i,x}X^{\langle i\rangle}+b_h)\rightarrow h^{\langle i\rangle}\rightarrow g(W_{i,h}h^{\langle i\rangle}+b_y)\rightarrow Y^{\langle i\rangle}$$

简化来讲，即：

$$\begin{align} X^{\langle 1\rangle}\xrightarrow{W_{x,h}}&h^{\langle 1\rangle}\xrightarrow{W_{h,y}}Y^{\langle 1\rangle}\\ &\downarrow W_{h,h}\nonumber \\ X^{\langle 2\rangle}\xrightarrow{W_{x,h}}&h^{\langle 2\rangle}\xrightarrow{W_{h,y}}Y^{\langle 2\rangle}\\ \end{align}$$

计算公式：

$$\begin{align} h^{\langle t\rangle}&=g_1(W_{x,h}X^{\langle t\rangle}+W_{h,h}h^{\langle t-1\rangle }+b_h)\\ y^{\langle t\rangle}&=g_2(W_{h,y}h^{\langle t\rangle}+b_y) \end{align}$$